Rody Félix & Dimitri Xanthoulis

Analyse de sensibilité du modèle mathématique “ Erosion Productivity Impact Calculator ” (EPIC) par l’approche One-Factor-At-A-Time (OAT)

Documenten bij dit artikel

Bijlagen

• pdf (314k)

Résumé

De nos jours, les modèles mathématiques deviennent très complexes et cette complexité se traduit, généralement, par une multiplication de leurs paramètres d’entrée (inputs). Cependant, ces derniers n’ont pas tous le même niveau d’influence sur les sorties (outputs). Dans le but d’identifier les paramètres les plus sensibles d’EPIC, ceux qui peuvent guider l’utilisateur dans la collecte d’informations sur le terrain et dans le processus de calibrage du modèle, une analyse de sensibilité par l’approche One-Factor-At-A-Time (OAT) a été effectuée sur deux jeux de données : l’un provenant du Programme-Action-Hesbaye (PAH, 1996) et l’autre du projet INCO (2000). La méthode utilisée consiste à modifier chaque entrée du modèle par –10 % et +10 % par rapport à sa valeur initiale. L’effet de chaque modification opérée est analysé sur six sorties d’EPIC, notamment : azote lessivé, eau percolée, eau consommée, biomasse, rendement et humus minéralisé dont la sensibilité est signifiée par le calcul d’un indice appelé “ Indice de Sensibilité ” et par un pourcentage de variation. En effet, les sorties considérées se montrent particulièrement sensibles aux paramètres “ Unités de chaleur potentielles ” (PHU), “ Fraction d’azote dans la plante à 50 % de maturité ” (BN2), mais surtout au “ Second point de l’évolution de la courbe du LAI ” (DLAP2). Une variation de 10 % de ce dernier provoque des changements moyens d’environ 14 % et 85 % sur les six sorties, respectivement pour les jeux de données du PAH et du projet Inco.

Abstract

Sensitivity analysis of the mathematical model “Erosion Productivity Impact Calculator” (EPIC) by approach One-Factor-At-A-Time (OAT). Nowadays, mathematical models are very complex and have many input parameters. Moreover, all do not have the same level of influence on the outputs. In order to identify the most significant parameters of EPIC that will guide the user on the field and in the process of calibration of the model, a sensitivity analysis by the approach One-Factor-At-A-Time was carried out on two data files: one coming from the “Programme-Action-Hesbaye” (PAH, 1996) and the other of the INCO project (2000). The method used consists in modifying each input parameter of the model by –10% and +10% around its initial value. The effect of each operated modification is analysed on 6 outputs of the model (nitrate leached, water percolation, water consumption, biomass, yield and mineralised humus) of which their sensitivity was quantified by calculation of an index called “Sensitivity Index” and by a percentage of variation. The outputs considered showed particularly sensitive to the parameters “Potential Heat Units” (PHU), “Fraction of nitrogen in plant at 50% of maturity” (BN2) but especially to the “Second point of the evolution of the LAI curve” (DLAP2). A variation of 10% of this parameter causes average changes of approximately 14% and 85% in the six outputs, respectively for the data files of the PAH and the Inco project.

Inhoudstafel

1. Introduction

1Les modèles mathématiques décrivant les phénomènes réels contiennent deux types d’incertitude : l’une qui est liée au modèle lui-même due à la description physico-mathématique inexacte du système et l’autre liée aux paramètres du modèle et due aux erreurs d’estimation et de procédure adoptée dans la collecte des données expérimentales utilisées (Ratto et al., 1996). En fait, les valeurs exactes des paramètres d’entrée d’un modèle ne sont jamais connues, et très souvent ont un important degré d’incertitude pouvant influencer sérieusement les prédictions même si le modèle est correct du point de vue physico-mathématique (Ratto et al., 1996). Ainsi, selon Saltelli et al. (1999), il est impératif pour l’utilisateur d’un modèle de chercher à savoir comment réagit son modèle par rapport aux facteurs d’entrée. Cette recherche de la compréhension du comportement d’un modèle vis-à-vis de ces paramètres, de la cohérence entre le modèle et le système qu’il représente et de la manière dont ses différentes parties interagissent, ne peut se faire que par le biais d’une analyse de sensibilité (AS) du modèle, qu’il soit numérique ou autre (Saltelli et al., 1999).

2Dans la littérature scientifique ayant trait à l’AS, on ne trouve pas vraiment une définition standard. Les définitions varient selon que l’objectif poursuivi est soit d’identifier un jeu de paramètres importants pouvant servir au calibrage d’un modèle, soit de juger de la qualité d’un modèle en essayant de repérer les fausses hypothèses posées lors de l’interprétation des phénomènes, soit d’identifier parmi plusieurs modèles celui ou ceux qui décrivent mieux un système réel donné. Cependant, selon Kleijnen (1995), l’AS peut être considérée comme une investigation systématique de la réaction d’un modèle vis-à-vis des valeurs extrêmes de ses paramètres ou des changements drastiques dans sa structure. Si dans certains cas la structure du modèle peut ne pas être remise en question, sa sensibilité ou le degré de variation des sorties par rapport aux incertitudes de ses paramètres d’entrée est d’importance et doit être connue. Selon Jolicoeur (2002), les paramètres dans un modèle mathématique complexe sont parfois très nombreux, et tous n’ont pas le même degré d’influence sur les sorties du modèle. Il y en a qui sont beaucoup plus importants que d’autres. Ainsi, une analyse de sensibilité peut aider à prédire l’effet de chaque paramètre sur les résultats du modèle et à les classer suivant leur degré de sensibilité (Saltelli et al., 2000a). La connaissance de cette information est très importante pour l’utilisateur d’un modèle, elle renseigne ce dernier sur le niveau de précision que doit avoir chaque paramètre et l’attention qu’on doit lui accorder lors de sa détermination sur le terrain ou au laboratoire (Jolicoeur, 2002).

3De nos jours différentes méthodes, les unes plus complexes que d’autres, existent pour effectuer l’analyse de sensibilité d’un modèle mathématique. Les trois principales utilisées sont : la “ Local Sensivity Analysis ” (LSA) la “ Global Sensivity Analysis ” (GSA) et le « Screening Designs (SD) ». Ces méthodes sont largement décrites dans Saltelli et al. (2000) et Kleijnen (1995) et vont être passées en revue brièvement dans le cadre de notre étude.

4La “ Local Sensitivity analysis ” s’attache à déterminer l’impact local des facteurs d’entrée sur le modèle. Elle repose sur le principe consistant à calculer les dérivées partielles des fonctions de sorties par rapport aux variables d’entrée. Ces calculs se font numériquement en faisant varier les entrées du modèle dans un intervalle très restreint autour d’une valeur nominale. Cette méthode peut être perçue comme un cas particulier de l’approche “ One-Factor-At-A-Time ” (OAT), car quand un facteur varie, tous les autres sont maintenus constants. Généralement, quand on applique cette méthode, les relations entre les entrées et les sorties sont supposées être linéaires et par conséquent, l’effet de la relative variation de la sortie du modèle en faisant varier le facteur d’entrée autour de sa valeur de base peut être estimée par la relation :

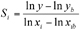
5(1)

6où Si est la mesure de sensibilité pour un facteur i donné, yb et y sont respectivement les sorties correspondant au facteur de base xib et au facteur xi (facteur de base augmenté ou diminué d’un certain pourcentage de variation).

7La “ Global SA ” est une méthode quantitative basée sur l’estimation de la contribution de chaque paramètre d’entrée d’un modèle à la variance observée dans les sorties ; elle étudie aussi l’interaction entre ces différentes variables d’entrée (Ratto et al., 2001 ; Soutter, Musy, 1999). Trois techniques principales sont largement utilisées : Monte Carlo (MC), “ Response Surface Methodology ” (RSM) et “ Fourrier Amplitude Sensivity Test ” (FAST). Ces techniques s’affranchissent des hypothèses classiques de linéarité que supposent les principes de régression et de corrélation.

8“ Screening Designs ” (SD) est la méthode la plus simple pour effectuer une analyse de sensibilité. Son but est d’isoler les facteurs les plus importants parmi de nombreux autres pouvant affecter une sortie particulière d’un modèle donné (Nearing et al., 1990). Le SD est très efficace quand le modèle à analyser a un nombre considérable de paramètres d’entrée (Jolicoeur, 2002). Trois types de technique peuvent être utilisés pour effectuer une AS par cette méthode : le “ One-Factor-At-A-Time ”, le “ Factorial Experimentation ” et le “ Fractional Factorial Experiment ”.

2. Approche et objet de l’étude

9Généralement, une analyse de sensibilité s’effectue en faisant varier certains paramètres d’un modèle autour d’une valeur connue déterminée au laboratoire ou sur le terrain, tout en gardant fixes les autres facteurs au cours de la simulation (Ma et al., 2000 cité par Jolicoeur, 2002). Le but de ce processus est d’arriver à identifier les paramètres d’entrée du modèle les plus sensibles, c’est-à-dire ceux pour lesquels une simple variation peut entraîner des changements considérables dans les sorties du modèle (Saltelli et al., 2000b). Dans cette étude la technique utilisée est l’approche OAT de la méthode “ Screening Designs ”. Son choix est basé sur le fait que son utilisation est assez aisée dans les modèles possédant de nombreux paramètres d’entrée, comme c’est le cas du modèle EPIC. Aussi faut-il signaler que les autres méthodes beaucoup plus complexes dans leur application, sont parfois plus efficaces dans l’analyse du comportement structurel de certaines zones d’un modèle (Local SA), ou font appel à des techniques de catégorisation des paramètres à tester de façon aléatoire (Global SA), ce qui limite un peu toute analyse exhaustive des réponses enregistrées vis-à-vis des incertitudes liées aux entrées du modèle.

10A travers cette démarche, on poursuit l’objectif d’analyser la sensibilité du modèle EPIC. Spécifiquement, on veut identifier les entrées qui contribuent le plus à la variabilité de six sorties du modèle notamment : la quantité d’azote lessivée, la quantité d’eau percolée en profondeur, la quantité d’eau consommée, la biomasse, le rendement et la quantité d’humus minéralisée. Ceci permettra de faire un classement des entrées les plus importantes du modèle EPIC et auxquelles une attention particulière doit être accordée lors de leur collecte ou de leur détermination sur le terrain.

3. Méthodologie

3.1. Présentation du modèle EPIC

11Erosion Productivity Impact Calculator (EPIC) est un modèle mathématique développé aux USA en vue d’établir la relation entre l’érosion du sol et la productivité. Il est conçu pour :

12– simuler simultanément des processus biophysiques en utilisant des données facilement disponibles ;

13– simuler des systèmes de culture sur de très longues durées afin de tenir compte du processus d’érosion qui est relativement lent ;

14– être appliqué à un large éventail de sols, de climats et de cultures ;

15– simuler les effets particuliers de pratiques de gestion sur l’érosion et la productivité du sol dans des environnements spécifiques.

16Dans EPIC on peut simuler les composantes suivantes : hydrologie, érosion-sédimentation, le cycle des nutriments, la croissance des plantes, le travail du sol, la température du sol, l’analyse économique et le contrôle de l’environnement de la plante. La description mathématique de toutes ces composantes est rapportée dans Sharpley et al. (1990).

17En utilisant ce modèle physique à pas de temps journalier comme outil d’aide à la décision, on peut apporter une aide substantielle dans l’identification, au niveau parcellaire, de stratégies optimales de gestion pour le drainage, l’irrigation, le contrôle de l’érosion, la fertilisation, le travail du sol, les dates de semis, la gestion des résidus de cultures, etc. (Cavero et al., 1996).

18Plusieurs types de données sont indispensables pour simuler un système à partir de ce modèle ; ce sont des données climatiques journalières ou des moyennes mensuelles, des données pédologiques (physiques et chimiques), des informations sur la gestion du système (fertilisation, irrigation, type de culture, date de semis et de récolte, etc.) et des paramètres biométriques des cultures produites dans le système. Plus de 200 entrées sont nécessaires pour faire tourner le modèle. Et les sorties générées sont tout aussi nombreuses. Des informations précises sur les entrées et sorties du modèle sont données dans Williams et al. (1990).

3.2. Données de terrain utilisées et démarche suivie

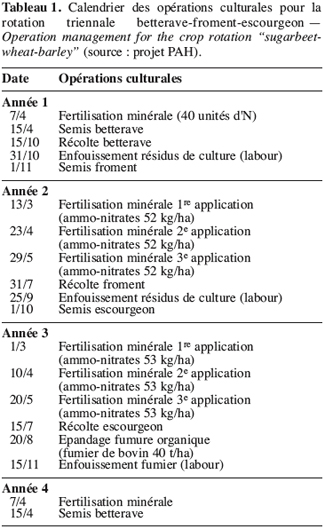
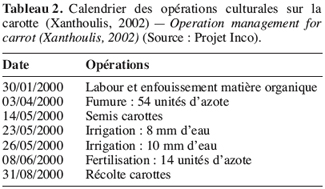
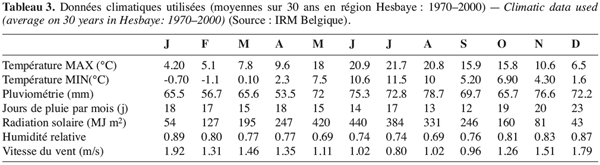
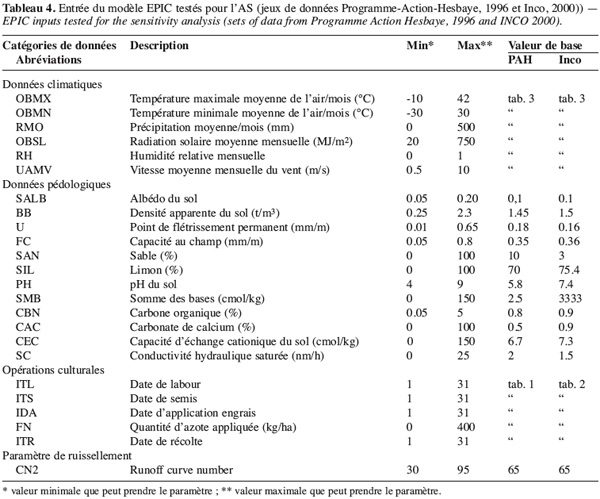
19Les données utilisées pour cette analyse de sensibilité proviennent, d’une part, d’une étude réalisée par l’unité “ hydraulique agricole ” de la FUSAGx dans le cadre du Programme-Action-Hesbaye qui visait à quantifier et à déterminer l’origine des nitrates percolant dans la nappe aquifère de Hesbaye et à étudier les modalités de transport des nitrates d’origine agricole vers la nappe (Dautrebande et al., 1996), et d’autre part, du projet “ Inco et suivi des irrigations ” (Xanthoulis et al., 2000). Les données relatives aux pratiques de gestion des agriculteurs (au calendrier des opérations culturales) ont été collectées pour les dix dernières années précédant l’étude (Tableaux 1 et 2). Les données climatiques utilisées sont les moyennes mensuelles sur 30 ans reprises au tableau 3. Les diverses données relatives aux propriétés physico-chimiques des sols de la zone sont indiquées dans la colonne “ valeur de base ” du tableau 4.

20La méthode utilisée consiste à modifier alternativement chaque entrée du modèle issue des jeux de données cités ci-dessus par –10 % et +10 % autour de sa valeur initiale ; ce pourcentage est considéré comme acceptable par rapport aux imprécisions probables liées aux paramètres d’entrée du modèle EPIC (Favis-Mortlock, Smith, 1990). De telles imprécisions peuvent être issues soit de certaines variabilités inhérentes à une mesure quelconque sur le terrain, soit de l’utilisation de données non représentatives du site de simulation. Un total de 355 simulations est effectué sur le jeu de données obtenu du Programme-Action-Hesbaye. Chaque simulation effectuée ne prend en compte que la modification d’une seule entrée par rapport à la globalité des paramètres du modèle. L’effet de chaque modification opérée est analysé au niveau des six sorties du modèle EPIC mentionnées plus haut soit : la quantité d’azote lessivée, la quantité d’eau percolée en profondeur, l’eau consommée, la biomasse, le rendement et la quantité d’humus minéralisée.

21Dans le modèle EPIC certains paramètres d’entrée ne peuvent pas être modifiés par +10 % et –10 % par rapport à leur valeur initiale. Par exemple, les dates concernant des opérations comme le labour, le semis, etc. doivent être des nombres entiers ; ainsi on les change en avançant ou en reculant les dates par +3 et –3 jours : erreur probable en spécifiant des données de ce type (Favis-Mortlock, Smith, 1990). Les entrées qui ont des valeurs zéro ou fixes et celles qui ont rapport avec l’érosion ne sont pas testées dans notre cas. Tout le long du processus, on a pris la précaution de ne modifier qu’une seule entrée par simulation.

22Les paramètres d’entrée du modèle qui feront l’objet de cette analyse sont classés en quatre catégories :

23– les paramètres climatiques,

24– les paramètres physicochimiques du sol,

25– les entrées liées aux pratiques de gestion (Tableau 4)

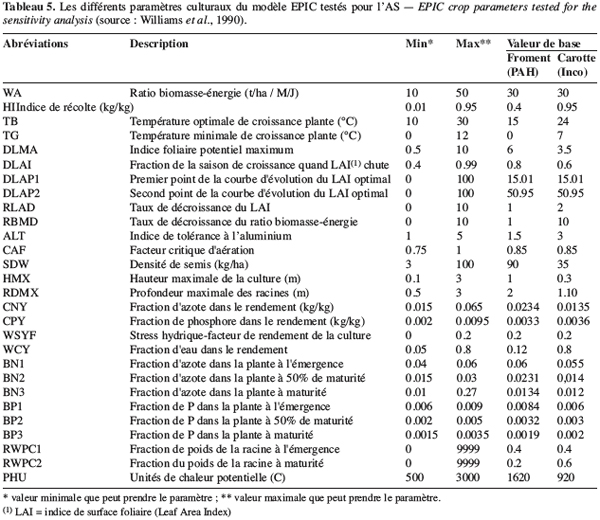
26– et les paramètres culturaux (Tableau 5). Les valeurs de base de ces paramètres sont obtenues des jeux de données issues des programmes cités ci-dessus.

27Les sorties du modèle sont traitées de la façon suivante :

281. En fait, la modification de chaque variable d’entrée par +10 % et –10 % produit deux valeurs pour chacune des six sorties retenues. De ces deux valeurs d’entrée, celle produisant la plus grande variation au niveau d’une sortie donnée est retenue pour l’évaluation et par conséquent pour le calcul de son indice de sensibilité (IS).

292. Dans le modèle EPIC les variables en rapport avec le climat telles que la température, la pluviométrie, la radiation solaire, etc., nécessitent une entrée pour chaque mois (moyennes mensuelles encodées dans notre cas), 12 au total ; et celles en rapport avec le sol une entrée pour chaque couche, 10 au total. Dans ce cas, la valeur du paramètre qui produit la plus grande variation sur n’importe quelle sortie, parmi les six considérées, est retenue. Elle devient la valeur choisie pour l’ensemble des 12 (climat) ou des 10 (sol) (Favis-Mortlock, Smith, 1990).

303. Un pourcentage de variation (Favis-Mortlock, Smith, 1990) et un indice de sensibilité (Jolicoeur, 2002) sont calculés pour chacune des sorties sélectionnées ci-dessus. Ils sont obtenus par les formules suivantes :

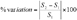
31(2)

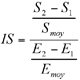
32(3)

33où

34IS est l’indice de sensibilité de la sortie du modèle ;

35E1 le paramètre d’entrée de base ;

36E2 la valeur testée (+10 % ou –10 %) ;

37Emoy la moyenne entre E1 et E2 ;

38S1, S2 sont respectivement les sorties correspondant à E1 et E2 ;

39Smoy est la moyenne entre S1 et S2.

40Cet indice permet d’avoir une base quantitative pour exprimer la sensibilité des sorties du modèle vis-à-vis des variables d’entrée. Un indice de sensibilité égal à 1 indique que le taux de variation d’un paramètre donné entraîne le même taux au niveau des sorties ; une valeur négative indique que les entrées et les sorties varient en sens inverse et plus grand est l’indice en valeur absolue plus grand est l’impact qu’un paramètre donné pourra avoir sur une sortie spécifique.

41En outre, un autre jeu de données issu du “ projet INCO” et du suivi des “ Irrigations à Waremme (Hesbaye), 2000 ” où des eaux usées sont utilisées comme complément sur des cultures maraîchères, a fait également l’objet de simulations. La culture simulée est la carotte et les résultats sont utilisés à des fins de comparaison. La même méthode adoptée pour l’analyse du jeu de données issu du Programme Action-Hesbaye (PAH) a été considérée, mais toutes les entrées n’ont pas été testées. Le choix de ces paramètres était fait au hasard ou orienté par les résultats obtenus de l’AS des données issues du PAH.

4. Résultats et analyse

42En modifiant de 10 % les entrées du modèle provenant du jeu de données du Programme-Action-Hesbaye, plusieurs d’entre elles produisent des variations non négligeables au niveau des sorties considérées dans le cadre de cette analyse de sensibilité. Seules les entrées produisant des changements de 0,5 % minimum sont prises en considération.

4.1. Sensibilité de la sortie “ Nitrate lessivé ”

43La modification des entrées du jeu de données produit des changements allant de 5 à 33,3 % au niveau de la sortie “ Nitrate lessivé ”. DLAP2, PH, FC, OBMX et PHU sont celles qui influent le plus sur cette sortie (Figures 1A et 1B). Elles induisent des variations respectives de 33,3, 23,8, 19, 14,3 et 14,3 %. Pour ces cinq entrées la sortie “ Nitrate lessivé ” accuse des indices de sensibilité allant de 1,3 à 3. Elle apparaît beaucoup plus sensible à l’entrée DLAP2 avec un IS de 3 suivie par PH, FC, OBMX et PHU.

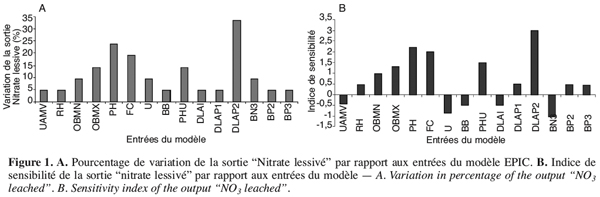
44Cette analyse montre que des incertitudes assez importantes sur ces paramètres peuvent fausser énormément les résultats obtenus pour la sortie “ Nitrate lessivé ”. En effet, il est bien connu que plus une plante se développe, plus élevée est sa demande pour l’élément “ azote ” ; et par conséquent, il est fort probable que l’azote minéral du sol soit absorbé de manière intense par les racines et du coup réduit le risque de lessivage. En revanche, ce risque peut être accentué au tout début de croissance de la plante car les besoins sont moindres. Voilà pourquoi les paramètres culturaux, DLAP2 et PHU, liés respectivement à la croissance maximale et au stade de développement de la plante, ont une telle influence sur le lessivage. Cependant, les incertitudes sur ces paramètres et en particulier sur le DLAP2 peuvent être relativement importantes. En effet, la précision du DLAP2 dépend de la rigueur de la méthode et de la technique adoptées dans la mesure de l’indice de surface foliaire (LAI). Les mesures indirectes via des instruments à capteurs optiques accusent généralement des marges d’erreur se situant entre 5 et 15 % pour un instrument comme “ LAI-2000 ” (Welles, Norman, 1991) et entre 0 et 50 % pour MODIS (Dungan, Ganapol, 2003). Au vu de ces erreurs qui peuvent dépasser la variation de 10 % adoptée, des stratégies de mesure bien élaborées s’imposent pour minimiser les incertitudes sur le LAI. Une autre option consiste à se tourner vers les mesures directes plus précises mais très lourdes à mettre en œuvre sur de grandes surfaces cultivées.

45Outre le DLAP2 et le PHU, la sortie en question est également assez influencée par l’incertitude au niveau du paramètre capacité au champ du sol (FC). Généralement dans les modèles de type fonctionnel, le profil du sol est décrit comme un ensemble de réservoirs successifs (horizons ou couches) dont chacun a une limite inférieure et une limite supérieure déterminant ainsi sa capacité de rétention en eau. En effet, dans EPIC, le paramètre FC est considéré comme la limite supérieure, c'est-à-dire la limite au-delà de laquelle l’eau coule d’un réservoir à un autre situé à un niveau inférieur. De ce fait une imprécision sur FC peut soit augmenter la capacité de stockage du réservoir ou la diminuer, ce qui, indubitablement, influera sur la quantité d’eau qui devrait traverser un point quelconque dans le profil du sol. étant donné que l’eau est le vecteur de transport des nitrates, il est normal qu’une incertitude trop élevée (10 %) sur ce paramètre ait un tel impact sur le lessivage de l’azote nitrique (19 %).

46Les principales sources d’incertitude sur ce paramètre résident, comme d’ailleurs c’est le cas pour la quasi-totalité des paramètres pédologiques, dans sa variabilité spatiale, dans l’imprécision, la non représentativité et l’insuffisance des données (Meyer et al., 1999). D’après Dautrebande et Casse (1999), ce paramètre peut accuser un coefficient de variation de 3 à 8 % dans certaines zones de la région Hesbaye.

47Le lessivage se révèle aussi sensible à la variation du paramètre OBMX, qui est une entrée liée à la température maximale. En fait les températures de 15 à 20 °C jouent un rôle important dans la disponibilité de l’azote dans le sol. Elles se révèlent idéales pour la minéralisation des fertilisants organiques apportés, donc une augmentation du stock azoté du sol ; mais aussi elles peuvent contribuer à la dénitrification dans le cas d’un sol bien arrosé, donc une diminution de l’azote disponible. Comme la disponibilité en azote est un facteur de risque de lessivage, surtout dans les régions bien arrosées, il est évident qu’une modification de OBMX influera sur la quantité de nitrate lessivé.

4.2. Sensibilité de la sortie “ Eau consommée ”

48Les figures 2A et 2B montrent que DLAP2, PHU, DLAP1 et OBSL sont les entrées les plus importantes en ce qui concerne la sortie “ Eau consommée par la plante ”. DLAP2 produit une variation de 9 % environ, PHU de 1,6 %, DLAP1 de 1,6 % et OBSL de 1,4 % avec des indices de sensibilité respectifs de –0,98, 0,15, 0,12 et 0,15 pour la sortie. à remarquer que l’IS obtenu pour l’entrée DLAP2 est négatif, ce qui montre que le paramètre varie en sens inverse de la sortie en question.

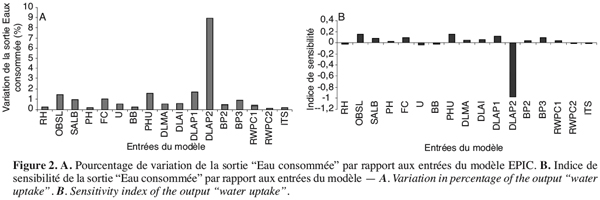
49Dans EPIC, les paramètres culturaux DLAP1 et DLAP2 sont utilisés pour générer l’indice de surface foliaire (LAI) qui est corrélé positivement avec l’évapotranspiration des plantes. Toute mesure incertaine de cet indice sur le terrain induira des erreurs sur les deux paramètres, erreurs qui fausseront par conséquent la sortie “ Eau consommée ”. Le même raisonnement est également vrai pour le PHU, lié au nombre de degrés-jours accumulés, qui détermine le stade végétatif de la plante. L’encodage d’un nombre de degrés de chaleur accumulée incorrect peut faire basculer la phénologie de la plante dans un stade inapproprié et influera, comme le montre l’analyse, sur la quantité d’eau consommée.

50Quant à l’entrée “ radiation solaire ” (OBSL) qui exerce son influence sur la sortie “ Eau consommée ”, elle est considérée comme l’un des plus importants facteurs climatiques qui affectent l’évapotranspiration potentielle (ETP). Dans EPIC, cette dernière est la base sur laquelle repose le calcul de la consommation hydrique des plantes. Ainsi toute erreur sur l’OBSL se répercutera sur la quantité d’eau évapotranspirée par la plante. à signaler que dans les stations climatiques règlementées, très peu d’incertitude plane sur cette entrée, comme d’ailleurs pour la grande majorité des paramètres climatiques. La marge d’erreur possible réside, généralement, dans l’extrapolation de certaines mesures à distance au site faisant l’objet d’étude.

4.3. Sensibilité de la sortie “ Eau percolée en profondeur ”

51La sortie “ Eau percolée ” subit beaucoup plus l’influence du DLAP2 et du CN2 comme l’attestent les figures 3A et 3B. Les variations respectives provoquées sont de 7 et de 4 %. La sensibilité de cette sortie vis-à-vis de ces deux entrées accuse des IS respectifs de 0,72 et –0,42.

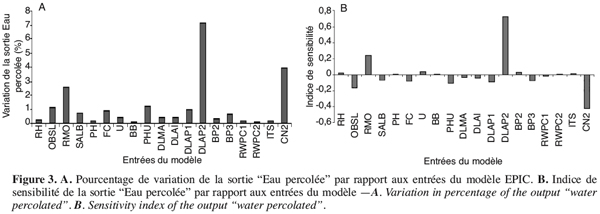
52Comme on l’a fait remarquer dans les paragraphes 4.1. et 4.2., le DLAP2 est le paramètre de contrôle de la croissance maximale de la plante. On sait que pendant cette période, l’indice de surface foliaire de la plante est très développé, ses besoins en nutriments augmentent pour permettre l’élaboration des produits photosynthétiques nécessaires, ce qui induit des besoins hydriques importants. Ainsi pour faire face à cette demande, la plante, via ses racines, absorbe intensivement l’eau qui se trouve dans le sol et par conséquent réduit la quantité d’eau percolée au-delà de la zone racinaire.

53D’après l’analyse, la percolation de l’eau est également influencée par le CN2, un paramètre qui gouverne le ruissellement. Dans le modèle, il est calculé selon la méthode du Soil Conservation Service (SCS) des USA qui prend en compte les aspects de surface (l’occupation du sol et les pratiques culturales), la pédologie (classes hydrologiques des sols) et le relief (pente). En fait, plus ce paramètre est grand, plus important est le ruissellement, ce qui influencera à coup sûr l’infiltration ou la quantité d’eau percolée. Des imprécisions planent toujours sur ce paramètre ; cependant cette AS montre, dans une certaine limite, que son influence est assez faible. En effet une incertitude de 10 % ne provoque qu’une variation de 4 % au niveau de la sortie testée.

4.4. Sensibilité de la sortie “ Rendement ”

54Les entrées BB, HI, DLAP2 et RWPC1 apparaissent comme celles pouvant influencer le plus la sortie “ Rendement ”. Elle accuse pour chacune d’elles des variations de l’ordre de 11 % et un indice de sensibilité égal environ à 1 pour les deux premières et -1 pour le DLAP2 et la RWPC1. Ce dernier montre que le taux de variation de ces entrées entraîne un même niveau de changement sur le rendement qui varie inversement aux DLAP2 et RWPC1 (Figures 4A et 4B).

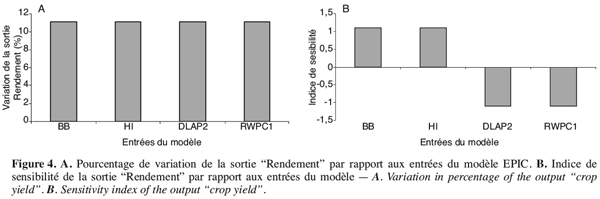
55En fait, il parait normal que le DLAP2 ait cette influence sur le rendement car c’est l’un des principaux paramètres qui contrôlent le niveau maximal dans la croissance de la plante. Une incertitude sur cette entrée pourrait avoir des répercussions sur de nombreux facteurs tels que : absorption d’eau, prélèvement d’éléments minéraux, etc. qui eux à leur tour influeront sur la quantité d’éléments photosynthétiques fabriqués ou le rendement. Pour le paramètre BB, densité du sol, son emprise sur la sortie peut trouver son explication dans l’effet de compactage du sol. En effet les sols compactés, donc de densité plus élevée, limitent le développement racinaire et par conséquent affectent considérablement l’alimentation hydrique et minérale des plantes indispensable à une bonne production.

56Quant à HI, indice de récolte, l’explication de son effet sur le rendement est purement numérique. Dans le modèle, il est défini comme étant le rapport entre le rendement économique et la biomasse aérienne. Cet indice est égal à 1 ou proche de 1 dans le cas d’une culture où toute la partie aérienne est considérée comme le rendement économique (épinard par exemple) ou nettement inférieur à 1 pour le froment par exemple. C’est une bonne connaissance de la culture à simuler qui permettra de choisir un indice correct pour réduire l’incertitude et en conséquence obtenir un rendement acceptable via le modèle.

57Le dernier paramètre RWPC1 qui influe également sur la sortie, est fixe dans le modèle. On peut admettre qu’aucune incertitude n’y est liée, car il ne fera jamais l’objet de détermination expérimentale.

4.5. Sensibilité de la sortie “ Humus minéralisé ”

58La variation de 10 % des entrées semble ne pas avoir trop d’influence sur l’humus minéralisé en se référant aux figures 5A et 5B, sauf BB qui provoque une modification de 8,5 % qui peut être expliquée par l’effet de portance ou de compactage du sol (influence sur la disponibilité en oxygène), et DLAP2 qui induit un changement assez faible de 3 %. Ces deux paramètres affichent des indices de sensibilité respectifs de 0,85 et de 0,32.

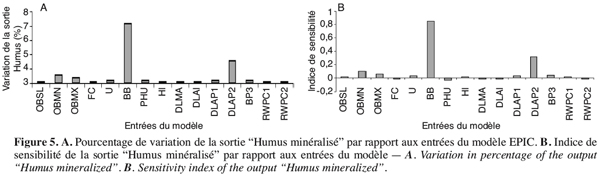
4.6. Sensibilité de la sortie “ Biomasse ”

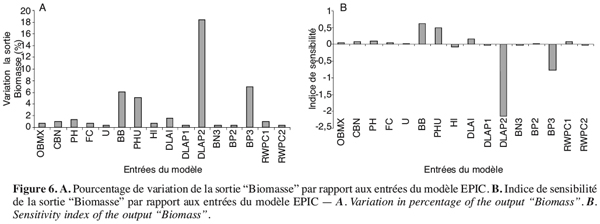
59La “ Biomasse ” paraît assez sensible à l’entrée DLAP2 et très peu sensible à la variation des autres. En effet une variation de 10 % du DLAP2 induit un changement de 18,5 % au niveau de la sortie. Signalons aussi que cette dernière varie en sens inverse du DLAP2 et accuse un IS de –2,13 environ (Figures 6A et 6B). L’interprétation concernant l’influence du DLAP2 sur la sortie “ Rendement ” est valable pour la biomasse, car, dans le modèle, le rendement est considéré comme un pourcentage de la biomasse.

4.7. Comparaison des variations des six sorties

60Une variation moyenne déterminée pour les six sorties considérées et ce pour chacune des entrées montre que DLAP2 est le paramètre le plus important avec une variation moyenne produite d’environ 14 %. Il est suivi de PHU, BB, PH et FC dont les variations se situent entre 5,9 et 3,2 %. La variation des autres entrées a très peu d’influence sur les sorties du modèle (Figure 7).

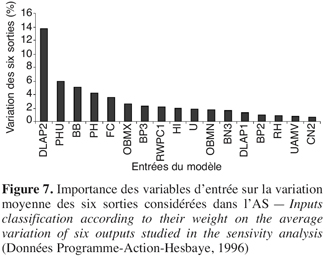
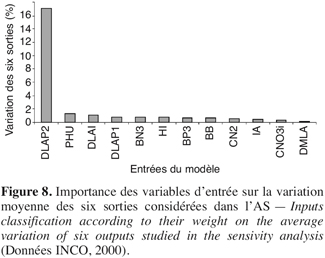
61La comparaison des résultats de l’analyse de sensibilité obtenus du jeu de données du Programme-Action-Hesbaye et ceux du projet INCO montre une certaine similarité quant à la sensibilité des six sorties choisies face à la variation des entrées du modèle de + ou -10 % par rapport à leur valeur initiale. En effet pour le jeu de données du projet INCO, les six sorties sont largement influencées par le DLAP2 suivi par PHU, DLAI, etc. (Figure 8). A signaler que pour ce dernier jeu de données, la variation moyenne produite par le DLAP2 (85 %), dépasse largement celle provoquée par le DLAP2 (14 %), pour ce qui est du jeu de données du Programme-Action-Hesbaye.

5. Conclusion

62La méthode utilisée, simple dans son application, consommatrice de temps mais très appropriée pour ce modèle dont les paramètres sont relativement nombreux, montre effectivement que toutes les entrées n’ont pas la même influence sur les sorties d’un modèle. Certaines sont plus importantes que d’autres, c’est-à-dire celles pour lesquelles une petite variation peut provoquer des changements considérables sur les sorties du modèle. En effet les sorties “ Nitrate lessivé ”, “ Eau consommée par la plante ”, “ Eau percolée en profondeur ”, “ Biomasse ”, “ Rendement ” et “ Humus minéralisé ” se montrent particulièrement sensibles au DLAP2, un paramètre dérivé des courbes LAI établies tout le long du cycle cultural d’une plante donnée. Une variation de 10 % provoque un changement qui varie entre 14 % et 85 % sur les six sorties respectivement du jeu de données PAH (1994) et du projet INCO (2000).

63En comparant les résultats des deux jeux de données, cette étude montre que la sensibilité d’un modèle vis-à-vis de ses paramètres est variable et assez relative. Elle peut subir des changements importants d’un jeu de données à un autre, comme peuvent l’attester les figures 7 et 8. Si en termes de grandeur les différences sont frappantes entre les résultats des deux jeux de données, en revanche une similarité assez nette est observée en ce qui concerne l’influence de certaines entrées du modèle EPIC sur les sorties considérées dans le cadre de cette analyse de sensibilité (Figures 7 et 8).

64Selon Favis-Mortlock et Smith (1990), les résultats d’une analyse de sensibilité doivent être manipulés avec précaution. En effet, la sensibilité apparente d’un modèle à un paramètre donné dépend de l’importance, durant la période choisie, du processus que ce paramètre affecte, elle-même liée aux contraintes environnementales et, dans une moindre mesure, aux conditions initiales. S’il ne pleut presque pas durant la période choisie, le modèle semble insensible aux paramètres impliqués dans le lessivage, constatation qui n’a pas lieu si les précipitations sont abondantes ou si l’irrigation pratiquée dépasse la capacité de rétention du sol.

65Cette AS montre aussi que toutes les catégories d’entrée : paramètres climatiques, pédologiques, culturaux, etc., peuvent influencer d’une façon ou d’une autre les résultats du modèle. Ceci sous-entend que des données assez précises doivent être encodées pour espérer des sorties fiables qui reflètent la réalité du système donné. En effet, si pour les paramètres climatiques, l’incertitude peut être faible (par exemple 0,2 % environ pour la température d’après Mölders, 2001) car les stations météorologiques sont assez standardisées et parfois très proches des sites d’étude, par contre pour les autres catégories (paramètres culturaux et pédologiques) les incertitudes peuvent être relativement importantes. Une erreur minimale de 4 % peut être observée pour la grande majorité des paramètres qui caractérisent un sol (Amy et al., 2002). Ce minimum d’incertitude recherché dépendra des méthodes expérimentales adoptées, du nombre d’échantillons collectés, des appareils utilisés et aussi de l’expérience de l’expérimentateur ou du technicien.

66En somme, la technique One-Factor-At-A-Time a ses limites, car changer un seul paramètre à la fois sous-entend que la modification opérée n’a aucune influence sur d’autres paramètres. Ce qui n’est pas une description exacte du monde réel ; par exemple un changement au niveau du paramètre “ pourcentage de limon ” du sol peut se répercuter sur le paramètre “ capacité au champ ”, mais cela n’est pas pris en considération. En fait, on se focalise beaucoup plus sur le comportement des sorties vis-à-vis d’une erreur relativement importante qu’on peut enregistrer dans les paramètres d’entrée pris isolément.

67Ainsi, dans le cadre de cette étude, les résultats obtenus donnent une idée assez claire des entrées les plus importantes du modèle EPIC. Ils peuvent guider l’utilisateur lors du processus de calage et aussi dans la collecte expérimentale des données. Toutefois, une étude approfondie sur l’incertitude des paramètres d’entrée du modèle pourrait se révéler très utile et viendrait renforcer cette analyse de sensibilité.

68Somme toute, le DLAP2, le paramètre le plus sensible d’après cette AS, doit être relativement précis pour espérer des prévisions réalistes. Dépendant essentiellement du LAI, ce dernier doit être mesuré dans de bonnes conditions de terrain et avec des méthodes fiables dont les plus notables sont les suivantes :

69– Les campagnes de mesure du LAI le long du cycle de la culture doivent être réalisées à des intervalles assez rapprochés (par exemple chaque semaine pour les cultures à cycle court) de telle sorte qu’on ait un maximum de points lors de la représentation de la courbe d’évolution du LAI. Cavero et al. (1998) ont suggéré six mesures au cours d’un cycle cultural.

70– Etant donné que les paramètres culturaux du modèle EPIC doivent être déterminés dans des conditions potentielles de terrain, il faut œuvrer en sorte que les mesures du LAI soient effectuées sur des plantes en situation de non stress hydrique, minéral, etc. En plein champ on peut penser à utiliser les plantes les mieux développées.

71– Avant d’utiliser les instruments à capteurs optiques qui mesurent indirectement le LAI (méthode non destructrice de la plante), il est conseillé de procéder d’abord par des mesures directes (méthode destructrice). Les données recueillies par cette méthode peuvent servir à calibrer au mieux l’instrument pour une utilisation efficace ultérieurement.

Bibliographie

Om dit artikel te citeren:

Over : Rody Félix

Over : Dimitri Xanthoulis