Amani Louis Kouadio, Bakary Djaby, Grégory Duveiller, Moussa El Jarroudi & Bernard Tychon

Cinétique de décroissance de la surface verte et estimation du rendement du blé d'hiver

Document(s) associé(s)

Annexes

• pdf (794k)

Résumé

La prise en compte de la diminution de la surface verte utile et de sa relation avec des processus biotiques et abiotiques pourrait s'avérer primordiale dans le développement de futurs modèles de prévision des rendements de blé dans le contexte actuel de réchauffement climatique. Dans notre étude, la phase de décroissance de la surface verte du blé d'hiver (Triticum aestivum L.) est suivie à travers le GAI (Green Area Index), variable calculée à partir de photographies hémisphériques prises sur différentes parcelles en Belgique, au Grand-Duché de Luxembourg et en France. La cinétique de décroissance de cette variable est décrite à l'aide de deux fonctions d'ajustements (les fonctions Gompertz et logistique modifiées). Les paramètres issus de ces fonctions et caractérisant la phase de décroissance (i.e. la valeur maximum du GAI, le taux de sénescence et le temps mis pour atteindre soit 37 % ou 50 % de la surface verte utile en phase décroissante du GAI) sont mis en relation avec les rendements observés. Les modèles élaborés montrent que le rendement final en grains peut être bien estimé à partir de ces paramètres, avec un coefficient de détermination (R²) de l'ordre de 0,83 et un RMSE de 0,48 t·ha^-1. Ces différents résultats rendent cette étude particulièrement intéressante pour une application dans un système opérationnel d'estimation du rendement du blé d'hiver à une échelle nationale ou régionale, l'estimation précoce de la production agricole à ces échelles étant plus que jamais au cœur d'enjeux économiques, géostratégiques et humanitaires importants.

Abstract

Estimating winter wheat yield through the decreasing phase of its green area. A large number of agrometeorological models for crop yield assessment are available with various levels of complexity and empiricism. However, the current development of models for wheat yield forecasting does not always reflect the inclusion of the loss of valuable green area and its relation to biotic and abiotic processes in production situation. In this study the senescence phase of winter wheat (Triticum aestivum L.) is monitored through the GAI (Green Area Index), calculated from digital hemispherical photographies taken over plots in Belgium, Grand-Duchy of Luxembourg and France. Two curve-fitting functions (modified Gompertz and modified logistic) are used to describe the senescence phase. Metrics derived from these functions and characterizing this phase (i.e. the maximum value of GAI, the senescence rate and the time taken to reach either 37% or 50% of the green surface in the senescent phase) are related to final grain yields. The regression-based models calculated with these metrics showed that final yield could be estimated with a coefficient of determination of 0.83 and a RMSE of 0.48 t·ha^-1. Such simple models may be considered as a first yield estimates that may be performed in order to provide a better integrated yield assessment in operational systems. Indeed, estimation of cereal-crop production, particularly wheat, is considered as a priority in most crop research programs due to the relevance of food grain to world agricultural production.

Table des matières

1. Introduction

1La sénescence des feuilles constitue une phase normale du cycle de développement des espèces. Au cours de cette phase s'installent des processus irréversibles de dégénérescence des structures et des fonctions cellulaires qui conduisent à une détérioration des tissus et des organes, et finalement à la mort de ceux-ci ou de l'organisme lui-même (Thomas et al., 1980). Chez les espèces annuelles, la sénescence peut se développer en l'absence de toute condition extérieure défavorable mais le froid, la sècheresse, l'ombrage, l'élimination de certains organes de la plante ou la présence de pathogènes peuvent l'induire et l'accélérer. La description de la sénescence a fait l'objet de plusieurs études, de même que sa modélisation dans les modèles de croissance des cultures (Gabrielle et al., 1998 ; Borrás et al., 2003 ; Lizaso et al., 2003 ; Duchemin et al., 2008). Ce phénomène physiologique de la plante est alors expliqué par des relations plus ou moins complexes, les formalisations choisies reposant le plus souvent sur des analogies connues ou sur la simplification de formalisations plus complexes.

2Dans le contexte actuel du réchauffement climatique et de ses conséquences sur l'homme et son environnement, l'estimation précoce de la production agricole aux échelles nationale ou régionale est plus que jamais au cœur d'enjeux économiques, géostratégiques et humanitaires importants. Dans cette optique, les modèles opérationnels pour la prévision des rendements pourraient exploiter l'information disponible durant la phase de croissance correspondant à la diminution de la surface verte utile et liée au remplissage des grains. Ce qui n'est pas le cas pour l'instant. Plusieurs modèles d'estimation et/ou de prévision de rendement du blé existent, à différentes échelles et avec des degrés divers de complexité et d'empirisme (Bouman et al., 1996 ; Bannayan et al., 2003 ; Brisson et al., 2003 ; Van Ittersum et al., 2003). De manière générale, la connaissance et la modélisation de la croissance de la surface foliaire sont d'une grande importance dans les modèles agrométéorologiques, d'autant plus que la production de biomasse et donc le rendement, dépendent essentiellement de l'activité photosynthétique de la plante.

3Deux types de méthodes de mesures de l'indice de surface foliaire (Leaf Area Index, LAI) existent : les méthodes directes et les méthodes indirectes. Une revue des méthodes est donnée dans Gower et al., 1999 ; Kussner et al., 2000 ; Jonckheere et al., 2004 ; Weiss et al., 2004. Les premières (méthodes directes) sont en général destructives, couteuses en temps et en main-d'œuvre car pour être précises, elles nécessitent la collecte d'un grand nombre d'échantillons (Jonckheere et al., 2004). Elles sont toutefois nécessaires pour calibrer les approches indirectes qui mesurent la fraction de vide (ou interception de la lumière) de la canopée. En effet, les méthodes indirectes se basent sur une approche probabiliste de la distribution des feuilles (ou son complément, la fraction de trous) et de l'architecture de la canopée pour le calcul du LAI (Weiss et al., 2004). Non destructives, elles utilisent pour la plupart des capteurs optiques. Pour les types de couverts végétaux pour lesquels il est difficile de séparer les feuilles et les autres organes du fait de l'architecture de la plante (i.e. le blé), d'autres notions sont utilisées pour caractériser la surface concernée de la biomasse. Ainsi, la notion de Plant Area Index (PAI) est utilisée quand tous les éléments de la plante sont inclus dans l'interception du rayonnement à travers la canopée (Neumann et al., 1989 ; Bréda, 2003 ; Hosoi et al., 2009). Plus particulièrement chez le blé, la notion de surface verte utile de la plante à travers le Green Area Index (GAI) se justifie par le fait qu'elle prend en compte l'ensemble des tissus de la plante photosynthétiquement actifs – feuilles, tiges et épis – (Olesen et al., 2002 ; Lawless et al., 2005 ; Baret et al., 2010 ; Duveiller, 2011). Parmi les méthodes de mesures indirectes du GAI, la photographie hémisphérique est de plus en plus utilisée de nos jours pour l'étude des structures des couverts végétaux (Demarez et al., 2008), notamment avec l'avènement de la photographie numérique qui offre de nombreuses possibilités de traitements. Toutefois, la détermination des valeurs de GAI à partir de photographies hémisphériques peut être soumise à certaines sources d'erreurs, notamment celles liées aux conditions de prises de vue ou celles liées au calcul de la fraction de trous du couvert influencé par la distinction des feuilles à l'ombre d'un sol foncé par exemple, ou la classification des pixels sur les images, etc. La photographie hémisphérique apparait néanmoins comme étant la méthode optique ayant le plus grand potentiel pour mesurer efficacement la fraction de trou car elle permet de capturer l'information sur la position, la taille, la densité des vides dans le couvert, et également les différences liées à l'architecture, à l'âge, de l'espèce végétale (Jonckeere et al., 2004).

4La mise en relation des variables biophysiques avec le rendement final chez le blé (Triticum aestivum L.) a fait l'objet de plusieurs études, notamment à travers l'évaluation quantitative du LAI, de la biomasse ou encore du pourcentage de couverture de sol par les indices de végétation au cours du cycle de croissance (Guyot et al., 1988 ; Laguette et al., 1997 ; Moulin et al., 1998 ; Glenn et al., 2008). Dans le domaine de la protection phytosanitaire de la culture du blé d'hiver, les travaux effectués durant ces dernières décennies ont montré l'étroite relation entre le temps durant lequel les dernières feuilles déployées demeuraient vertes lors du remplissage des grains et le rendement final (Gooding et al., 2000 ; Reynolds et al., 2000 ; Richards, 2000 ; Dimmock et al., 2002 ; Blandino et al., 2009 ; El Jarroudi et al., 2010), l'activité photosynthétique des dernières feuilles de blé contribuant pour environ 30 à 50 % des assimilats utiles au remplissage des grains (Sylvester-Bradley et al., 1990). Ainsi, le paramètre « m » tiré de la fonction d'ajustement Gompertz modifiée, qui donne le moment du point d'inflexion de la courbe décroissante de la surface verte utile du blé, était corrélé significativement au rendement final en grains (Gooding et al., 2000 ; El Jarroudi et al., 2010). Le début et la vitesse de sénescence des dernières feuilles déployées constitueraient alors d'importants facteurs dans l'estimation précoce du rendement final en grain chez le blé. Mais du fait de la prise en compte uniquement des dernières feuilles déployées, les conclusions de ces études peuvent s'avérer difficiles à mettre en œuvre pour un suivi à des échelles plus larges en condition opérationnelle. Les systèmes d'estimation ou de prévisions actuellement utilisés dans des contextes opérationnels incluent implicitement la phase de sénescence dans l'élaboration finale du rendement par le biais des modèles agrométéorologiques inclus dans ces systèmes. Quelques exemples sont donnés par Supit (2000), Bannayan et al. (2003), Brisson et al. (2003) et Confalonieri et al. (2009). Les conclusions des études sur la relation étroite entre la sénescence des dernières feuilles déployées et le rendement final suggèrent que cette relation est mal exploitée et pourrait être mieux valorisée dans un contexte opérationnel. En ce sens, un suivi direct et régulier du couvert végétal organisé à une échelle départementale ou régionale fournirait les données nécessaires à l'élaboration d'un modèle décrivant au mieux la phase de décroissance de la surface verte et pourrait relier ces paramètres caractéristiques de la courbe de décroissance (appelés « metrics ») au rendement final.

5Notre étude explore une piste de valorisation d'une des conclusions de l'étude de Gooding et al. (2000) qui montrait une relation très significative entre la phase de sénescence et le rendement final du blé d'hiver : il s'agira ici d'estimer le rendement final du blé à partir des metrics dérivés de la phase de décroissance du GAI à l'échelle parcellaire, et de faire ressortir l'applicabilité d'une telle démarche dans un contexte opérationnel.

2. Matériel et méthodes

2.1. Mesures de terrain

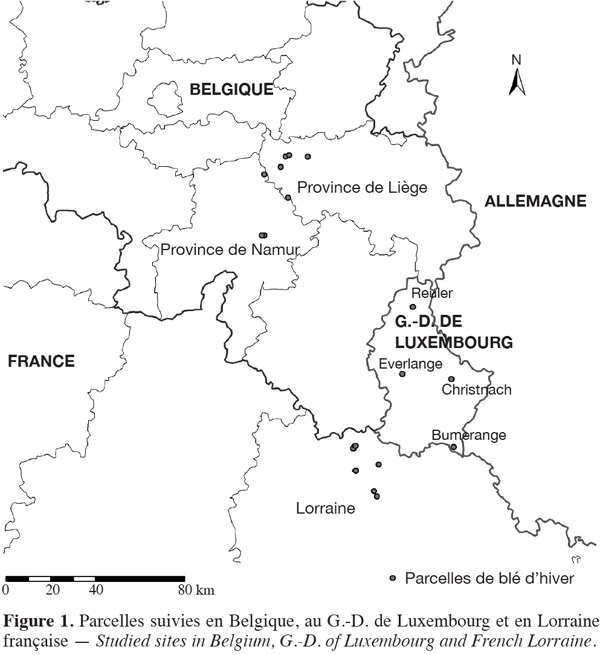
6La campagne de terrain pour la collecte des données a eu pour cadre des champs de blé d'hiver localisés en Belgique, au Grand-Duché de Luxembourg et en Lorraine française durant la saison de culture 2008/2009 (Figure 1). La période de suivi retenue dans notre étude s'étend du mois de mai au mois de juillet 2009, période pendant laquelle la surface verte de la plante atteint son maximum avec le développement de toutes les feuilles, puis accomplit sa phase de décroissance. Les suivis de la phénologie et de la phase de décroissance de la surface verte ont lieu durant la période s'étalant du stade GS 23 (stade « talles visibles ») au stade GS 90 (stade « maturité complète ») de l'échelle de Zadoks (Zadoks et al., 1974). Les images hémisphériques desquelles sont extraites la variable biophysique d'intérêt, le GAI, sont prises à l'aide d'un appareil photonumérique muni d'une lentille hémisphérique du type « fish-eye » (BESEL Fisheye wide range 0.25x lens). Ces prises d'images sont faites à la verticale au-dessus de la canopée (comme recommandé par Demarez et al., 2008), à environ 60 cm pour le blé jeune et 70-90 cm pour le blé mature, selon la variété. Sur les sites du G.-D. de Luxembourg et de la Lorraine française, l'appareil photonumérique utilisé est du type CANON Powershot A590 (3 264 x 2 448 pixels). Sur les sites en Belgique, deux appareils ont été utilisés : un appareil photonumérique CANON Powershot A590 (3 264 x 2 448 pixels) et un appareil de type CANON Powershot A540 (2 816 x 2 112 pixels). Les différents appareils photonumériques et la lentille fish-eye ont été calibrés suivant la méthode décrite sur le site https://www4.paca.inra.fr/can-eye pour le calcul du centre optique de la lentille hémisphérique.

7Parcelles suivies au Grand-Duché de Luxembourg. Au G.-D. de Luxembourg, les prises ont été effectuées sur des sites expérimentaux d'une étude portant sur les avertissements pour le contrôle des maladies de blé, notamment la septoriose, l'oïdium et la rouille brune (El Jarroudi et al., 2009). Les différents cultivars concernés sont 'Cubus', 'Boomer', 'Achat' et 'Schamane' (Tableau 1). Trois niveaux de traitements fongicides (triple, double et aucun traitement), avec quatre répétitions, sont pris en compte sur chaque site. Les produits fongicides appliqués sont essentiellement constitués de mélanges de triazoles et de strobilurines. Les différents mélanges, de même que les stades phénologiques d'applications des produits fongicides, sont donnés dans le tableau 2.

8La dimension de chaque parcelle étant de 8 m x 1,5 m, trois photographies hémisphériques furent prises sur chacune d'elle à différents endroits (à un intervalle de 1,5 m en moyenne le long de la parcelle). Le traitement des photographies pour dériver la valeur de GAI par niveau de traitement fongicide est fait sur le lot total des photographies correspondant à chaque niveau de traitement, soit 12 photographies. Les fréquences temporelles de prises de vue sont reprises dans le tableau 3. En moyenne, ce sont deux prises de vues qui sont effectuées tous les 10 jours tout au long de la période de décroissance suivie. Pour chaque parcelle, le rendement est évalué après pesée de la production totale en grains ramenée à la surface réelle récoltée. La récolte est effectuée à l'aide d'une moissonneuse batteuse pour parcelles (type Delta, WINTERSTEIGER). Le prélèvement de la totalité de la parcelle est fait en cabine et la masse des grains fournie avec une précision de ± 100 g. Cette masse est ensuite ramenée à la surface réelle récoltée pour déterminer le rendement de la parcelle donnée, en prenant en compte le taux d'humidité des grains (inférieur à 15 %). La moyenne des rendements des quatre parcelles par niveau de traitement est ensuite prise en compte pour les analyses statistiques ultérieures.

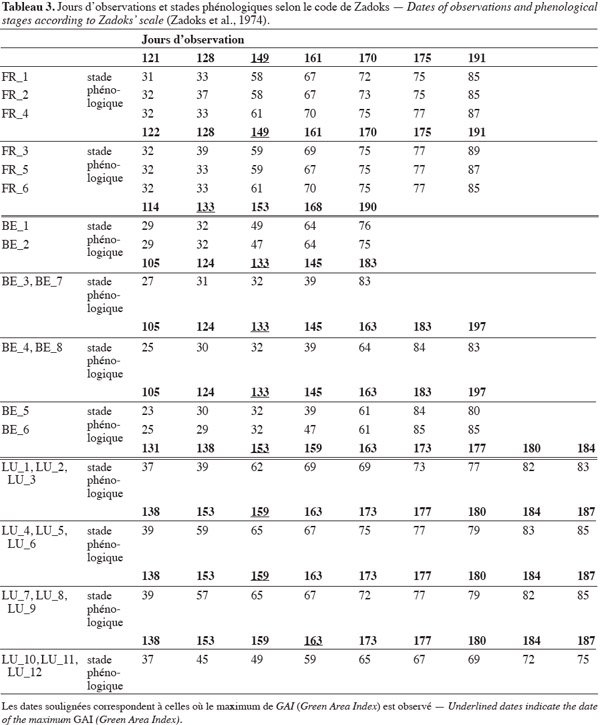
9Parcelles suivies en Belgique et en Lorraine française. En Belgique et en Lorraine française, la campagne de terrain s'inscrivait dans le cadre du projet GLOBAM1 (GLOBal Agricultural Monitoring systems by integration of earth observation and modeling techniques). Les sites sont choisis selon des critères définis dans le cadre dudit projet, notamment l'acquisition d'images satellitaires moyennes et hautes résolutions et d'images radar (fréquence de passages, couverture spatiale, etc.), la représentativité en termes de productivité du blé d'hiver dans la zone ou la région de culture, etc. À la différence des parcelles du G.-D. de Luxembourg, les champs suivis en Belgique et en Lorraine française sont des champs en exploitation normale. Les cultivars de blé pour les champs de la Lorraine française et de la Belgique sont repris dans le tableau 1.

10Les tailles des champs suivis dans ces deux zones variaient entre 5 et 30 ha. En fonction de la taille du champ, au minimum 10 photographies hémisphériques réparties sur une zone représentative du champ (de taille approximative de 50 m x 50 m) étaient prises (15 pour les champs de plus grande surface). Chaque série de photographies ainsi constituée est censée représenter la variabilité de la canopée de chaque champ (Weiss et al., 2004). Une seule valeur de GAI est dérivée après traitement de chaque série de photographies ainsi obtenue. Les prises de vue en Belgique et en Lorraine française sont effectuées en moyenne tous les 10 jours tout au long de la période de croissance suivie (Tableau 3). Pour chaque site, les champs retenus pour la suite des analyses sont ceux pour lesquels le rendement fut évalué par l'agriculteur après pesée de la production totale de grains en fin de saison (lors de la mise en silo) ramenée à la surface du champ. Les récoltes ont été effectuées sur ces parcelles à l'aide de moissonneuses batteuses, généralement de type CLAAS Lexion. Au total, sur plus d'une trentaine de parcelles suivies dans ces deux zones (Figure 1), ce sont seulement six pour la Lorraine française et huit pour la Belgique qui ont été retenues (Tableau 1).

2.2. Traitement des photographies hémisphériques

11Le traitement des photographies hémisphériques est effectué avec le logiciel CAN-EYE (https://www4.paca.inra.fr/can-eye). Ce logiciel permet de calculer notamment le PAI à partir de la fraction de trou que constitue l'espace sans végétation. Cette fraction est estimée à partir d'une classification supervisée réalisée sur un lot de photographies. Une description détaillée des équations qui sous-tendent les calculs effectués par ce logiciel est donnée dans Weiss et al. (2004) et Demarez et al. (2008). Dans le cadre des analyses avec le logiciel CAN-EYE, la variable d'intérêt dérivée est le « green » PAI (i.e. GAI), la classification ayant lieu en utilisant uniquement deux classes : « verte » et « pas verte » (incluant le sol et la végétation non verte). En effet, la prise des photographies au-dessus de la canopée prenant en compte tous les organes de la plante, la classe « verte » se réfère à l'ensemble des feuilles, tiges et épis verts.

2.3. Ajustement de fonctions aux courbes de décroissance du GAI

12Pour caractériser l'évolution temporelle du LAI (calculé à partir d'indices de végétation) d'un couvert de blé, Baret et al. (1986) ont proposé un modèle paramétrique combinant un modèle logistique simple modélisant la phase de croissance de la culture et un modèle exponentiel négatif caractérisant la phase de sénescence de la plante. Gooding et al. (2000) ont montré que la sénescence des dernières feuilles émergées du blé est bien caractérisée par une fonction Gompertz modifiée. Étant donné que l'objectif de notre étude est de valoriser une des conclusions de l'étude précédente, et pour apprécier leur capacité à décrire l'évolution décroissante du GAI chez le blé, les fonctions Gompertz modifiée (Équation 1) et logistique modifiée (Équation 2) proposées par Gooding et al. (2000) seront utilisées pour décrire la phase de décroissance du GAI.

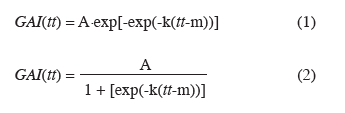
13où A désigne le pourcentage initial du GAI, m (exprimé en degrés par jour) est le moment où le point d'inflexion de la courbe apparait, k exprime le taux de dégénérescence du GAI et tt, le temps thermique exprimé en degrés-jours.

14Lorsque A est fixé à 100 % (GAI est à sa valeur maximale), l'inflexion de la courbe lors de la phase décroissante apparait à GAI = 37 % pour la formule Gompertz modifiée (50 % pour la fonction logistique modifiée). Le temps thermique, tt, sur n jours se calcule comme suit :

15où T_ai (°C·j^-1) est égale à la moyenne journalière de la température de l'air. [T_ai = 0,5*(T_max + T_min)] ; T_b (°C·j^-1) étant égale à la température de base. Dans le calcul des cumuls, (T_ai - T_b) est égal à 0 lorsque T_ai < T_b. Pour le blé, T_b est fixée à 0 °C (Baker et al., 1980 ; Baker et al., 1983 ; Davidson et al., 1983 ; Masle et al., 1989). La période de calcul du temps thermique commence à la valeur maximale de GAI (GAI_max). Il est alors fixé à 0 à cette date et le cumul est effectué pour les jours suivants. Ainsi, le metric m représente le temps thermique nécessaire pour atteindre soit 37 % (Équation 1), soit 50 % (Équation 2) de la valeur de GAI restant depuis sa valeur maximale. Les variables climatiques, températures minimale (T_min) et maximale (T_max), sont issues de stations météorologiques proches des parcelles suivies (entre 1 et 5 km).

16La qualité des ajustements effectués est appréciée par la VAF (variance accounted for, proportion de variance expliquée). Elle se détermine par la formule suivante :

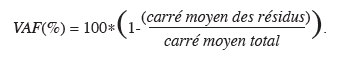
2.4. Élaboration des modèles d'estimation du rendement

17Les modèles sont déterminés par régression linéaire générale avec des sets de données se référant aux deux fonctions dont sont dérivés les metrics. Ainsi, le premier set d'inputs comprend les valeurs de m_gomp, k_gomp (fonction Gompertz modifiée), le GAI_max et les rendements observés. Le second set comprend les valeurs de m_log, k_log (fonction logistique modifiée), le GAI_max et les rendements observés. Une analyse des corrélations entre variables explicatives permet de dégager les variables non corrélées entre elles, de sorte à éviter la colinéarité dans la construction des modèles. Les modèles utilisés pour la validation sont ceux ayant au moins deux variables explicatives. La phase de validation de ceux-ci est effectuée à travers un bootstrap. Le bootstrap est une technique de rééchantillonnage permettant de simuler la distribution d'un estimateur quelconque pour en apprécier le biais et la variance, donc le risque quadratique ou encore pour en estimer un intervalle de confiance, même si la loi théorique de la distribution est inconnue (Palm, 2002). Cette méthode permet ainsi d'évaluer les performances des modèles de régression (Efron et al., 1993 ; Davison et al., 1997 ; Austin et al., 2004). Étant donné la nature des parcelles suivies (parcelles expérimentales et parcelles d'agriculteurs) des trois sites d'étude, les données seront traitées séparément dans l'élaboration des modèles d'estimation du rendement : celles du G.-D. de Luxembourg d'une part, et celles de la Belgique et de la Lorraine française de l'autre. Les traitements statistiques relatifs aux ajustements de fonctions et à la modélisation sont réalisés avec les procédures Proc NLIN et Proc GENMOD du logiciel SAS® (version 9.1.3 pack 2 ; SAS Institute Inc., Cary, NC).

2.5. Critères de choix du meilleur modèle

18La sélection des modèles est un problème bien connu en statistique. Lorsque le modèle est fixé, la théorie de l'information fournit un cadre rigoureux pour l'élaboration d'estimateurs performants. Mais dans un grand nombre de situations, les connaissances a priori sur les données ne permettent pas de déterminer un modèle unique dans lequel se placer pour réaliser l'inférence (Lebarbier et al., 2004). L'une des réponses apportées au problème de la sélection des modèles est la minimisation d'un critère pénalisé. Parmi ces critères, l'AIC (Akaike Information Criterion, [Akaike, 1973]) a été largement diffusé et appliqué (Sawa, 1978 ; Akaike, 1987 ; Bozdogan, 1987 ; Bozdogan, 2000). L'AIC permet de sélectionner un modèle optimal qui réalise le meilleur compromis biais-variance. Il se détermine selon la formule suivante :

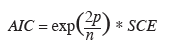
19où n est le nombre d'observations ; p désigne le nombre de paramètres, y compris l'intercept ; SCE est la somme des carrés des erreurs.

20Le meilleur modèle sera celui qui minimise le critère AIC. Deux autres critères de comparaison seront également pris en compte, à savoir l'erreur quadratique moyenne ou RMSE (root mean square error) et le R² ajusté (R²_aj). Le RMSE se détermine selon la formule suivante :

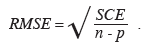
21Le R²_aj est une valeur corrigée du R² qui prend en compte l'influence liée au nombre de variables prédictives d'un modèle donné. Il se calcule selon la formule suivante :

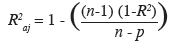
22avec R² désignant le coefficient de détermination.

3. Résultats

3.1. Ajustements des courbes de décroissance de GAI

23Les ajustements effectués sont globalement satisfaisants. Pour les données du G.-D. de Luxembourg, en moyenne la VAF est de 93 % pour chacune des deux fonctions d'ajustements. De même pour les données de la Belgique et de la Lorraine française, la moyenne est de 92 % et de 93 % respectivement pour la fonction Gompertz modifiée et la fonction logistique modifiée. Ce qui traduit une bonne caractérisation de la phase de décroissance par ces deux fonctions. La figure 2 donne les différentes VAF par les deux fonctions obtenues pour les sites sélectionnés.

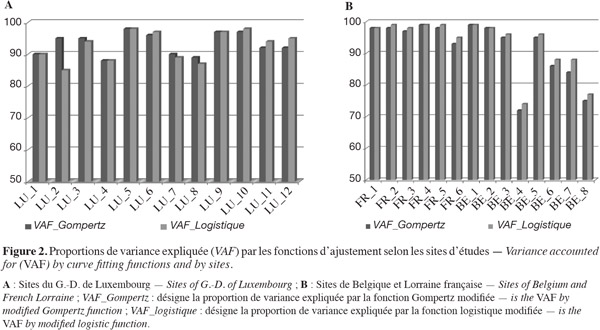
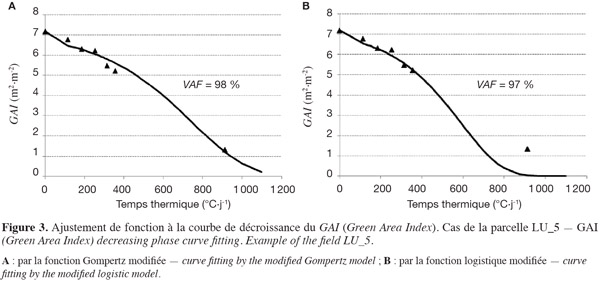
24Dans leur étude, Gooding et al. (2000) montrent que la phase de décroissance de la surface verte des dernières feuilles déployées est mieux caractérisée par la fonction Gompertz modifiée. En extrapolant cette conclusion à la description de la phase de décroissance de la surface verte utile de toute la plante, on constate que les deux fonctions – Gompertz et logistique modifiées – décrivent tout aussi bien cette phase. L'ANOVA réalisée entre les VAF par chaque fonction d'ajustement montre en effet que celles-ci ne sont pas significativement différentes (P = 0,731 pour les sites du G.-D. de Luxembourg et P = 0,716 pour les sites de Belgique et Lorraine française). Un exemple d'ajustement des fonctions aux valeurs de GAI est donné en figure 3.

3.2. Établissement des modèles d'estimation du rendement

25L'analyse des corrélations entre les variables explicatives du rendement a montré qu'aucune corrélation significative n'existait entre celles-ci, aussi bien entre les variables explicatives issues de la fonction Gompertz modifiée qu'entre celles issues de la fonction logistique modifiée pour l'ensemble des sets d'inputs. Quatre modèles sont ainsi évalués à partir du premier set d'inputs (fonction Gompertz modifiée) et quatre autres depuis le second set d'inputs (fonction logistique modifiée). Les différents termes des modèles évalués ainsi que leurs critères de performances sont repris dans les tableaux 4, 5 et 6.

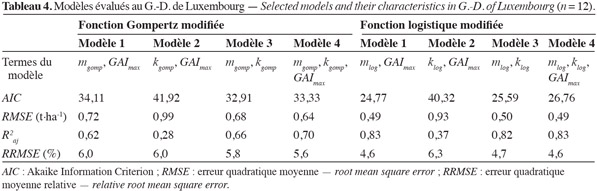
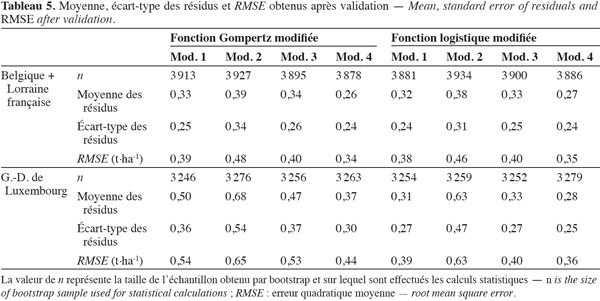
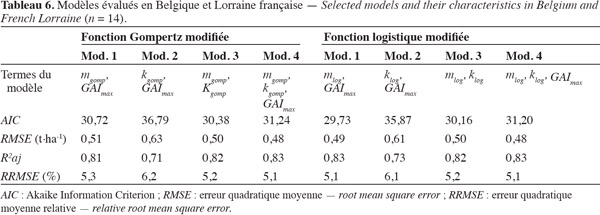
26En ce qui concerne les données issues des parcelles expérimentales du G.-D. de Luxembourg, les valeurs de R²_aj permettent une première comparaison entre les modèles. Ainsi, seuls les modèles ayant comme variables explicatives k_gomp / k_log et GAI_max présentent de mauvaises performances (faibles R²_aj et grandes valeurs de RMSE, tableau 4). Pour chaque fonction considérée, les trois autres modèles se rejoignent en termes de performances (AIC faibles et R²_aj élevés), plus particulièrement les modèles avec les variables explicatives issues de la fonction logistique modifiée (AIC variant entre 25 et 27, et R²_aj de 0,82/0,83). Le tableau 5 qui présente les principaux résultats obtenus après validation renforce cette conclusion. En effet, les différents RMSE sont faibles : entre 0,44 et 0,54 t^.ha^-1 pour les modèles Mod.1, Mod.3 et Mod.4 issus de la fonction Gompertz modifié et entre 0,36 et 0,40 t^.ha^-1 pour ces mêmes modèles issus de la fonction logistique modifiée.

27Les analyses effectuées avec les données des parcelles d'agriculteurs (Belgique et Lorraine française) ne montrent aucune grande différence entre les modèles évalués. D'une manière générale, ceux-ci présentent de bons critères de performances : des valeurs de R²_aj supérieures à 0,71 au minimum et des RMSE ne dépassant guère 0,63 t^.ha^-1 (Tableau 6), de faibles valeurs de RMSE après validation (Tableau 5). Bien qu'au niveau des données issues des parcelles expérimentales, de meilleures performances sont obtenues des metrics de la fonction logistique modifiée, aucune distinction nette ne peut être faite entre les deux groupes de modèles obtenus dans le cas des parcelles d'agriculteurs.

28En comparant dans leur ensemble les modèles issus des deux fonctions d'ajustement pour les parcelles expérimentales et les parcelles d'agriculteurs, cette étude montre que des modèles d'estimation du rendement final avec de bons critères de performances peuvent être obtenus. Les valeurs de AIC les plus faibles sont celles issues des modèles associant uniquement les metrics m et k de la courbe de décroissance (Tableaux 4 et 6). Les précisions des modèles obtenus sont quasiment les mêmes dans chaque cas de figure, avec toutefois les meilleures obtenues pour les parcelles du G.-D. de Luxembourg avec les metrics issus de la fonction logistique modifiée (de l'ordre de 4,6 % d'erreur, tableau 6). Cette différence de précision entre parcelles expérimentales et parcelles d'agriculteurs pourrait être imputée à la méthode d'évaluation du rendement final. En effet, au niveau des parcelles expérimentales, ces valeurs sont issues de la surface réelle récoltée, tandis qu'au niveau des parcelles d'agriculteurs, les valeurs de rendements sont évaluées à partir des surfaces emblavées.

4. Discussion et conclusion

29Dans cette étude, le suivi de la phase décroissante du GAI est réalisé à partir de photographies hémisphériques puis caractérisé par des paramètres tirés de deux fonctions d'ajustements (fonctions Gompertz et logistique modifiées). Bien que les photographies hémisphériques fournissent des informations pertinentes sur la structure de la canopée, la détermination des valeurs de GAI à partir de ces photographies reste soumise à certaines sources d'erreurs liées aux prises de vue ou au traitement des images (Duthoit, 2006 ; Demarez et al., 2008 ; Duveiller, 2011). Duthoit (2006) note que pour des photographies hémisphériques prises dans une culture de blé dans des conditions optimales (bonne représentativité de la canopée, 10 photographies au minimum, prises au-dessus de la canopée, grande résolution des images, et distance entre l'objectif et la prise de vue variant entre 45 et 70 cm), l'erreur quadratique moyenne sur les valeurs de LAI obtenues variait entre 0,15 et 0,33 m²·m^-². La comparaison des valeurs de GAI obtenues après traitement par le logiciel CAN-EYE et des valeurs de GAI obtenues par méthodes destructives n'a pas fait l'objet d'étude dans notre cas. Une quantification exacte de la gamme d'erreur pourrait bien faire l'objet de recherches futures. Par ailleurs, une première étude relative à l'élaboration d'une méthode automatique de traitement des photographies hémisphériques prises sur des cultures comme le blé par le logiciel CAN-EYE (Duveiller, 2011) a montré des résultats intéressants quant aux difficultés dans le traitement des photographies et aux difficultés d'interprétation de la notion de classe « verte » pour le calcul du GAI. À terme, la mise en place d'une méthode automatique robuste devrait réduire significativement les erreurs de subjectivité pouvant être induites par l'opérateur et réduire davantage le temps de traitement des photographies hémisphériques prises dans le cadre d'un suivi fréquent de plusieurs parcelles.

30Une autre conclusion intéressante de cette étude tient au fait que les phases de décroissance du GAI au niveau des parcelles sont bien décrites par les fonctions Gompertz et logistique modifiées (Figure 2). Le suivi de la phase de décroissance de la surface verte utile de la plante (à travers le GAI) est fait sur des parcelles en différents endroits du point de vue pédologique et météorologique (Belgique, G.-D. de Luxembourg et Lorraine française). De plus, les variétés de blé concernées et les pratiques culturales diffèrent également. Par exemple pour le G.-D. de Luxembourg, ce sont quatre variétés différentes qui sont utilisées, allant notamment des variétés sensibles aux variétés moins sensibles à la septoriose (El Jarroudi et al., 2009). La surface verte utile de la plante de blé et son évolution, exprimée à travers les valeurs de GAI, traduiraient ainsi l'influence combinée des facteurs agronomiques (variétés et pratiques culturales) et des facteurs environnementaux (climatiques, pédologiques, pression des maladies, etc.). L'estimation du rendement final sur base de la cinétique de sénescence du GAI constitue un premier pas dans la prise en compte de l'impact sur le rendement final des phénomènes pouvant subvenir lors de cette phase. Tout en vérifiant la qualité des ajustements des fonctions aux courbes de décroissance de GAI, les metrics dérivés de celles-ci sont mis en relation avec le rendement final observé. Les modèles obtenus présentent dans leur ensemble des critères satisfaisants pour une estimation du rendement final (Tableaux 4 et 6). De ce fait, la variabilité spatiale du rendement engendrée par les facteurs sus-énumérés est bien prise en compte et cela, à différentes échelles de prises de vues des photographies hémisphériques (parcelles expérimentales et parcelles d'agriculteurs). Toutefois, des analyses ultérieures sur plusieurs années de données devraient permettre de vérifier la robustesse d'une telle méthode pour l'évaluation de la variabilité inter-annuelle du rendement.

31Les comparaisons des performances des modèles dans notre étude ont montré que ceux associant uniquement les metrics m et k des fonctions de décroissance étaient statistiquement les meilleurs. Mais à performances égales, les modèles incluant également comme variable explicative le GAI_max (qui exprime un potentiel de croissance de la plante) seront choisis préférentiellement pour une estimation du rendement final. Ces différents résultats rendent cette étude particulièrement intéressante pour une application dans un système opérationnel d'estimation du rendement final du blé d'hiver à des échelles nationale ou régionale. La problématique toujours actuelle des systèmes opérationnels de prévisions de rendement (obtenues le plus tôt possible dans la saison) demande l'utilisation de modèles robustes, pouvant être appliqués en temps réel et à une grande échelle (> 10 000 km²) (Laguette et al., 1997). Malgré les avantages offerts par la télédétection spatiale (notamment le suivi régulier de la végétation sur de grandes étendues géographiques), les études utilisant des informations issues de celle-ci et spécifiques aux cultures dans un contexte opérationnel sont rares (Doraiswamy et al., 2007). L'une des difficultés majeures réside en effet dans le fait que les paysages agricoles sont généralement beaucoup plus fragmentés, avec des exigences variables en termes de résolution spatiale (Duveiller et al., 2010a). L'objectif de la présente étude n'est pas d'établir une comparaison entre les performances des différentes approches existantes. Elle s'est proposée plutôt de jeter les bases d'une alternative pour l'amélioration des prévisions de rendements à des échelles régionales sur base de modèles faisant intervenir très peu de variables (deux à quatre) et liés à la phase de sénescence du GAI. C'est en ce sens que l'approche a été testée à l'échelle de la parcelle à travers les valeurs de GAI issues de photographies hémisphériques. La relative simplicité de notre approche ne devrait toutefois pas être au détriment de son efficacité réelle, malgré les limitations que peut présenter toute approche empirique. En effet, l'approche détaillée dans cette étude appliquée à des valeurs de GAI dérivées d'images satellitaires multi-spectrales (Duveiller et al., 2010b) d'une saison de culture de blé à l'échelle des NUTS3 (Nomenclature des Unités Territoriales Statistiques, niveau 3 [http://epp.eurostat.ec.europa.eu/portal/page/portal/nuts_nomenclature/introduction]) sur une zone d'étude de 300 km x 300 km permettait d'obtenir des estimations de rendement final avec des erreurs quadratiques moyennes de 0,30 t^.ha^-1 (Kouadio et al., 2010). L'approfondissement d'une telle approche, qui valoriserait l'information de la télédétection spatiale, permettrait à terme de disposer de modèles simples et fiables d'estimation du rendement final dans un contexte opérationnel.

32Remerciements

33La campagne de terrain en France et en Belgique s'inscrivait dans le cadre du projet GLOBAM (GLOBal Agricultural Monitoring systems by integration of earth observation and modeling techniques) financé par les SSTC (Services Fédéraux des Affaires Scientifiques, Techniques et Culturelles, Belgique). Nous remercions l'équipe de l'Université Catholique de Louvain-la-Neuve pour la collecte et le traitement des données sur les sites belges, et également Messieurs Sébastien André et Frédéric Arnaud de la Chambre d'Agriculture de Meurthe-et-Moselle (France).

Bibliographie

Notes

Pour citer cet article

A propos de : Amani Louis Kouadio

A propos de : Bakary Djaby

A propos de : Grégory Duveiller

A propos de : Moussa El Jarroudi

A propos de : Bernard Tychon