Seyed Jalil Alavi, Kourosh Ahmadi, Carsten F. Dormann, Josep M. Serra-Diaz & Zahra Nouri

Assessing the dominant height of oriental beech (Fagus orientalis L.) in relation to edaphic and physiographic variables in the Hyrcanian Forests of Iran

Documenten bij dit artikel

Bijlagen

• pdf (730k)

Résumé

Évaluation de la hauteur dominante du hêtre oriental (Fagus orientalis L.) par rapport aux variables édaphiques et physiographiques dans les forêts hyrcaniennes d'Iran

Description du sujet. Cette étude évalue l'application des arbres à régression stimulée (BRT) pour prédire la hauteur dominante des hêtres dans les forêts hyrcaniennes en Iran, inscrites au patrimoine mondial de l'UNESCO en raison de leur remarquable biodiversité.

Objectifs. Il est largement admis que la croissance des arbres peut être influencée par une grande variété de facteurs tels que le climat, la topographie, les conditions du sol et la concurrence pour les ressources. Les premières études de modélisation de la hauteur dominante des arbres ont utilisé la régression linéaire multiple. Le développement de méthodes non paramétriques et d'apprentissage machine plus avancées a permis de surmonter les relations non linéaires dans les écosystèmes forestiers.

Méthode. Dans cette étude, des arbres à régression amplifiée ont été évalués pour modéliser la hauteur dominante de Fagus orientalis en tant qu'espèce d'arbre la plus importante dans la forêt hyrcanienne, en Iran. La hauteur dominante était liée aux variables pédologiques et topographiques, qui sont disponibles pour 190 placettes échantillons couvrant tous les gradients environnementaux importants dans la zone de recherche.

Résultats. Les résultats ont montré que les BRT étaient plus performants pour la modélisation de la hauteur dominante des hêtres. Cette technique a montré que le phosphore, le pourcentage d'azote, le magnésium et le pourcentage de sable étaient parmi les variables les plus importantes.

Conclusions. Cette étude démontre la capacité des BRT à modéliser avec précision la hauteur dominante du hêtre oriental par rapport aux prédicteurs environnementaux, et encourage son utilisation en écologie forestière.

Abstract

Description of the subject. This study evaluates the application of Boosted Regression Trees (BRT) for predicting beech dominant height in the Hyrcanian forests of Iran, inscribed as a UNESCO’s World Heritage due to its remarkable biodiversity.

Objectives. It is widely accepted that tree growth can be influenced by a wide variety of factors such as climate, topography, soil conditions and competition for resources. The early dominant height of trees modelling studies used the multiple linear regression. The development of more advanced non-parametric and machine learning methods provided opportunities to overcome the nonlinear relationships in forest ecosystems.

Method. In this study, boosted regression trees was evaluated to model the dominant height of Fagus orientalis as the most important tree species in the Hyrcanian forest, Iran. Dominant height was related to soil and topographical variables, which are available for 190 sample plots covering all importance environmental gradients in the research area.

Results. The results indicated BRT were found to outperform for modelling beech dominant height. This technique showed that phosphorus, percentage nitrogen, magnesium and percentage sand were among the most important variables.

Conclusions. This study demonstrates the ability of BRT to accurately model the dominant height of oriental beech in relation to environmental predictors, and encourages its use in forest ecology.

Inhoudstafel

1. Introduction

1Northern forests of Iran, called Hyrcanian or Caspian forests, cover a relatively narrow strip in the north of Iran, which are among the most important and valuable ecosystems inscribed in United Nations Educational, Scientific, and Cultural Organization (UNESCO) World Heritage List. Hyrcanian forests are important sources of genetic variation, biodiversity, commercial woody products, and of various environmental services (Ahmadi et al., 2013). Covering an area of about 1.85 million ha, these forests account for 15% of the total Iranian forests and 1.1% of the country’s area. These forests range from sea level up to an altitude of 2,800 m and comprise various forest types, harboring approximately 80 woody species (trees and shrubs). Oriental beech (Fagus orientalis Lipsky), chestnut-leaved oak (Quercus castaneifolia C.A.Mey.), velvet maple (Acer velutinum Boiss.), hornbeam (Carpinus betulus L.) and Caucasian alder (Alnus subcordata C.A.Mey.) are among the main tree species in these forests. Hyrcanian forests, along with similar North American and East Asian forest communities, are nowadays seen as remnants of contiguous Tertiary deciduous belt (Sagheb Talebi et al., 2014), and hence one of the world’s oldest extant forests. Today, these forests are regularly harvested, but their management is rarely based on assessments of growth, standing biomass or specific target forest composition and must, in places, be considered unsustainable.

2Sustainable forest management requires a reliable estimation of wood quantity and quality. For the range of stand densities usually targeted in forest management, dominant height is not dependent on stand density and responds little to forest thinning, so that it reflects site growing conditions better than mean height or stand basal area growth. Dominant height is thus considered an important variable for specifying stand development and predicting the growth potential of a site (von Gadow & Hui, 1999; Nunes et al., 2011). More specifically, dominant height, as proxy for growth potential, is affected by the soil’s chemical and physical characteristics, the topography and the climate at the stand level (Nambiar et al., 2004). Indeed, Remy de Perthuis de Laillevault in the 18^th century proposed the application of height growth for assessing site quality in forest stands, leading to the development of a site index (Vanclay & Skovsgaard, 1997; Batho & Garcia, 2006). Unlike diameter at breast height, mean height and volume, dominant height usually does not show sensitivity to silvicultural treatments and variations in the stand density (Curtis & Reukema, 1970; Hogg & Nester, 1991). The dominant height, due to close relationship with volume, is considered as a good site productivity index (Carmean, 1975; Hagglund, 1981; Clutter et al., 1983). A further important characteristic of dominant height is that its variability within sample plots which are used in site index studies is relatively low, but it shows high variability between sample plots; this latter component of variability is that which is expected to be linked to variations in the productivity of sites (Herrera et al., 1999).

3It is widely accepted that the growth capacity of forest species can be influenced by a wide variety of complex interacting factors including climate, topography, soil conditions and competition for resources (Assmann, 1970; Oliver & Larson, 1996). In both forest ecology (Coomes & Allen, 2007) and sustainable forest management (Pretzsch, 2009), an understanding of the variation in tree growth is important. Numerous studies have focused on climate, geologic, topographic and soil factors (Ung et al., 2001; Palahı et al., 2004; Seynave et al., 2005) or used indicator plants for site quality assessment and classification (La Roi et al., 1988; Berger & Walther, 2006).

4Understanding the main factors affecting on high and low production efficiency in forest areas is essential for both science and industry (Pretzsch et al., 2015). A better understanding also may contribute to design of forest production systems which are very important in sustainable forest management (Forrester, 2014). In many of the early studies, assessment of forest dominant height was related to environmental variables using multiple linear regression, mostly without considering non-linear effects and interactions among predictors; similarly, heterogeneous variances and distributional assumptions were regularly violated (Aertsen et al., 2010). The number and complexity of modelling techniques to cope with the inherent complexity of ecological problems has increased markedly over the past years (Moisen et al., 2006; Aertsen et al., 2010; Hegel et al., 2010). The development of advanced nonparametric and machine learning techniques and the growing availability to geodatasets with high spatial resolution have increased the accuracy for predicting forest characteristics (Aertsen et al., 2010).

5Many of machine learning algorithms have been used in different fields of forest science including classification and regression trees (CART), random forest (RF), boosted regression tree (BRT), artificial neural networks (ANN), support vector machine (SVM), cubist (Cubist) and multivariate adaptive regression splines (MARS). These data-driven methods have already been successfully applied to ecology and remote sensing to perform tasks such as species distribution (Alavi et al., 2019; Ahmadi et al., 2020a). However, the applications in forest growth and yield prediction are still limited. boosted regression trees (BRT) approach is a promising machine-learning technique, which is currently valuable tools for ecological modelling, and seems to be powerful tools for analyzing large datasets and identifying non-linear relationships (Drew et al., 2011). The performance of this model has been investigated by several authors in recent years, pointing to an overall suitability for a wide range of applications and data sets (Moisen & Frescino, 2002; McKenney & Pedlar, 2003; Segurado & Araujo, 2004; Elith et al., 2006; Elith & Graham, 2009; Aertsen et al., 2010; Oppel et al., 2012; França & Cabral, 2015).

6Oriental beech is an important late-successional and shade-tolerant species that occurs in mild mountainous or marine climates with high humidity. Although growing on every soil, beech trees are rare in moist and heavy soils (Tabari et al., 2005). The contents of loam play an important role in beech growth and height, so that the best beech forests in terms of diameter and height growth are located on semi-heavy and well-drained soils with sufficient moisture (Habibi Kaseb, 1974). Other studies found the importance of such characteristics as soil depth, silt, phosphorus, pH, bulk density and topographic variables as the main factors in distribution of beech communities (Salehi et al., 2005; Mataji et al., 2009). In terms of nutrients requirements of the oriental beech tree, there are contrasting studies. Regarding to the effects of physiography on beech trees, Marvi Mohajer (1976) found beech trees located at elevation between 900 to 1,500 m a.s.l. had the best status based on tree height (Marvi Mohajer, 1976). He emphasized the beech forests located in mid-lands of Caspian forests have higher forest site productivity. Beech trees prefer north-facing slopes and demand for atmosphere moisture and cool environment (Gorgi Bahri & Sagheb-Talebi, 1992; Sagheb-Talebi, 1996; Alavi et al., 2012).

7About 18% of the total forest area, 30% of the standing volume, and 24% of the stem number in Hyrcanian forests in Iran are occupied by beech forests. Because of the importance of oriental beech as the most valuable wood-producing species of Hyrcanian forests, in this study, we evaluated the dominant height of this species as an important indicator of forest productivity in relation to physiographic and edaphic variables using a well-known machine learning method (boosted regression tree). The results of present study allow forest managers to identify the main drivers of dominant height of beech trees obtained from machine learning models and have sustainable planning for the future of these forests.

2. Materials and methods

2.1. Study area

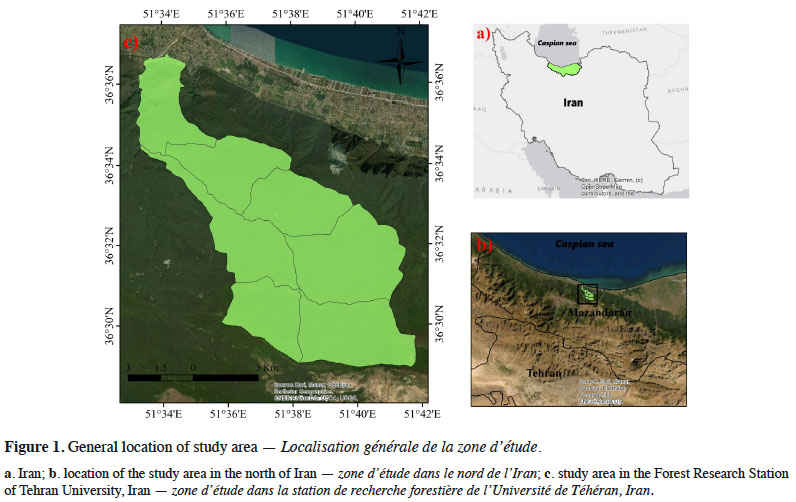
8This research was conducted in Kheyroud Forest of Mazandaran Province, Iran. The study area is managed by the Natural Resources Faculty of Tehran University, Iran. This forest is located on the Northern slopes of the Alborz Mountains, about 7 km east of the little sea-port of Nowshar, Caspian Sea (N 36.6, E 51.8). It measures about 10,000 ha and extends from 0 to 2,200 m above sea level. This forest is divided into seven districts and the present research has been conducted in Patom, Namkhaneh, Gorazbon, Chelir and Baharbon districts in an area about 6,500 ha (Figure 1). Mean annual rainfall is 1,368 mm with maximum and minimum falls in October and June, respectively. Temperatures vary from a mean monthly minimum of 2.6 °C in January and February to a maximum of 29.2 °C in June and July, with an annual mean of 16.2 °C (Alavi et al., 2012). This region has a semi-moist climate with cold winters according to the De Martonne climagram. The study area’s forests are mixed and uneven-aged, dominated by Fagus orientalis associated with Carpinus betulus, Acer velutinum, Parrotia persica C.A.Mey., Sorbus torminalis (L.) Crantz, Quercus castaneifolia, Alnus subcordata C.A.Mey., Acer laetum C.A.Mey., Prunus avium (L.) L., Ulmus glabra Huds. and Tilia begoniifolia Steven species. These forests are managed as close-to-nature with single tree harvesting methods.

2.2. Data collection

9A stratified sampling method based on landform extracted from DEM used to locate 190 circular sample plots of 0.1 ha in beech forests in the study area. Plots were established in sites without evidence of anthropogenic disturbances including forest harvesting. All trees with DBH > 7 cm were measured for diameter at breast height (DBH) using caliper to the nearest millimeter and total height of all beech trees was using Vertex IV (Haglöf, Sweden). Dominant tree height is defined as the average height of five highest trees within the sample plot.

10The summary of environmental variables are presented in Table 1. Slope (in %) of the plots in the study area was recorded by using a standard clinometer. Aspect, as the azimuth measured from true north, was transformed to a topographic radiation index using the equation TRASP = [1 – cos ((π/180) (θ – 30))]/2. This criterion assigns a value of zero to north-northeast facing slopes (typically the coolest and wettest orientation) and a value of one to the hotter and drier south-southwesterly slopes (Moisen & Frescino, 2002; Ahmadi et al., 2020b).

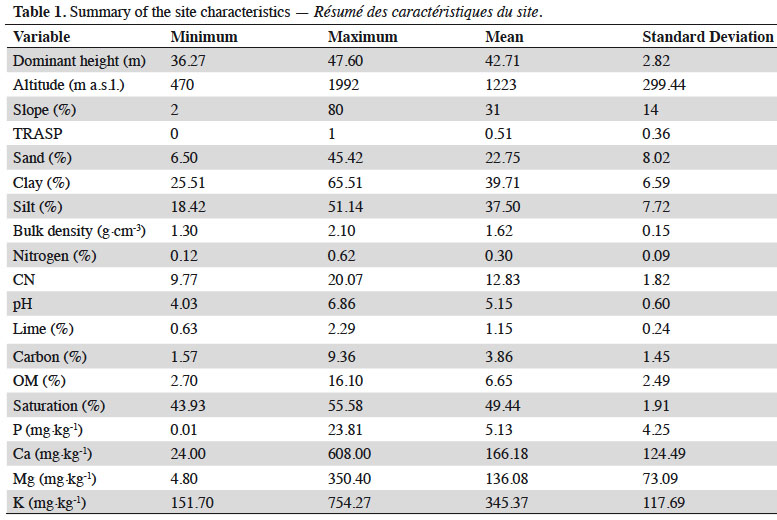
11For quantifying nutrient availability, five topsoil samples (0-20 cm) were randomly taken within each plot. Soil samples were mixed and analyzed in the laboratory. Roots, shoots and pebbles were separated by hand and discarded and the air-dried soil samples were sieved. Soil variables including physical and chemical properties were determined by the following methods: bulk density (by clod method; Plaster, 2013), texture by Bouyoucos hydrometer method (Bouyoucos, 1962), pH in water (soil: water ratio 1:2.5), total organic C by Walkley and Black method (Allison, 1965), total N by Kjeldahl method (Bremner & Mulvaney, 1982), the available P by using the Olsen method (Homer & Pratt, 1961), available K, Ca and Mg by a flame atomic absorption spectrophotometer (AA500F, PG Instruments Ltd, China), the proportion of CaCO₃ (total lime) by the Calcimeter method (Allison & Moodie, 1965).

2.3. Statistical methods

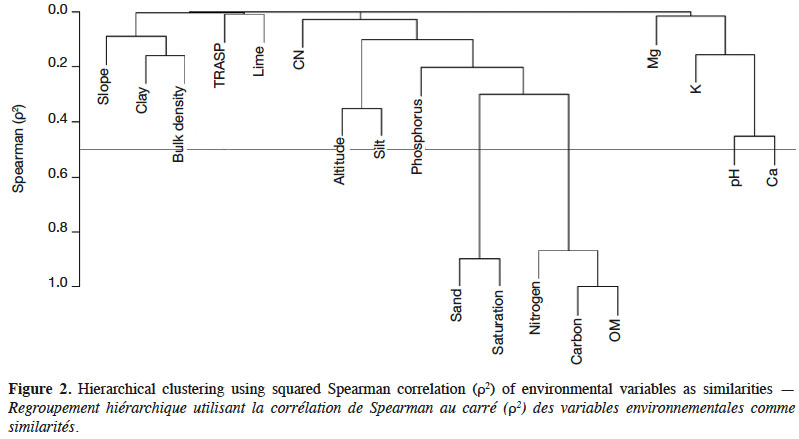
12The number of candidate variables included in the final model were firstly reduced by removing highly correlated variables. Collinearity among environmental predictors were tested by hierarchical cluster analysis using squared Spearman correlations with the Hmisc package (Harrell Jr et al., 2018) in the R statistical software (R Core Team, 2018). In case of collinearity problems, one of any pair of predictors showing such problems should be discarded for modelling purposes (Draper & Smith, 1998; Dormann et al., 2013). The variables percentage saturation, percentage carbon and percentage organic matters were hence removed from the set of predictors. We then applied develop predictive model for variation of beech dominant height using boosted regression trees (BRT) (Figure 2).

13The linear model was simplified using backward stepwise and bayesian information criterion (BIC), which considers both the goodness-of-fit and model complexity and penalizes model complexity more than the AIC (Burnham & Anderson, 2002) and has been argued to select for optimal explanation rather than optimal prediction. Classification and regression trees were created with the rpart package (Therneau & Atkinson, 2018) in the R statistical software. The resulted decision trees were pruned based on 10-fold cross-validation (McKenney & Pedlar, 2003).

14Boosted regression trees were fitted using the dismo package (Hijmans et al., 2017) with a fixed tree complexity of 3 (according to recommendations by Elith et al. [2008] for small datasets) and a bag fraction of 0.75 and learning rate 0.001 and Gaussian response type. The BRT model was then simplified by reducing the number of independent variables (Elith et al., 2008). Although the predictive importance of a variable can often be very insightful, most scholars are interested in how the variable is related to the outcome.

2.4. Evaluation of predictive performance of boosted regression trees

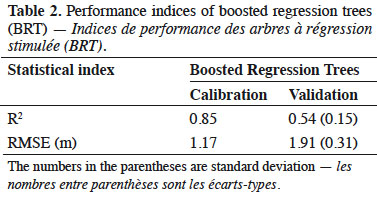
15Since there is no independent data to evaluate the predictive performance of the models, 10-fold cross-validation method was used to measure their performances. In 10-fold cross-validation, the data are split into 10 random subsets of equal size. The modelling technique is then applied 10 times; each time one of the subsets is left out and the prediction accuracy is calculated by using that subset. The procedure was replicated 100 times. Predictive performance of derived models is quantified by calculating model evaluation measures on the predicted values for cross-validation. The performance of models was measured in terms of coefficient of determination (R²) and the root mean squared error (RMSE). Finally, our ecological interpretation of optimal model relies on the assessment of the relative importance of the explanatory variables and their partial plots.

3. Results

16In the present study, we evaluated the dominant height of oriental beech, which is one of the most abundant species in the Hyrcanian forests of Iran, using a boosted regression tree model and edaphic and topographic variables. The results showed that 12 variables were influential, but phosphorus, percentage nitrogen, Mg and percentage sand had the highest effect on predicting the beech dominant height. Calcium and percentage clay were the least important variables in BRT. Large positive values indicate the variable is predictive, whereas zero or negative importance values identify variables not predictive (Ishwaran, 2007). Only few of the descriptors contributed noticeably to the estimation of beech dominant height, namely phosphorous, percentage of nitrogen, percentage of sand and Mg. The predictive performance in terms of coefficient of determination (R²) values of BRT model is in table 2. This study showed an improvement of ensemble method (BRT) with 58% in R² (Figure 3).

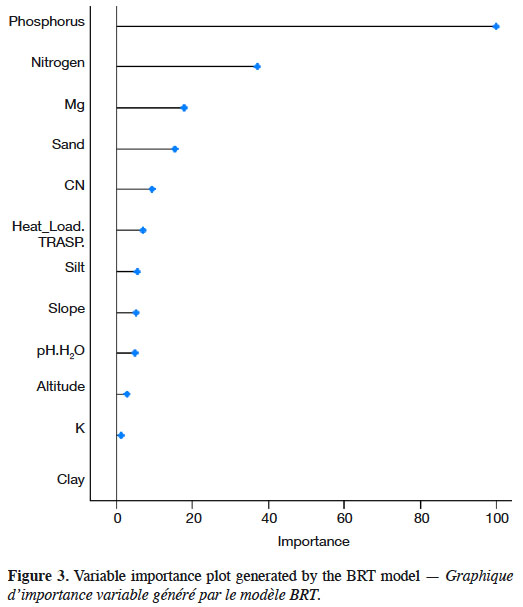
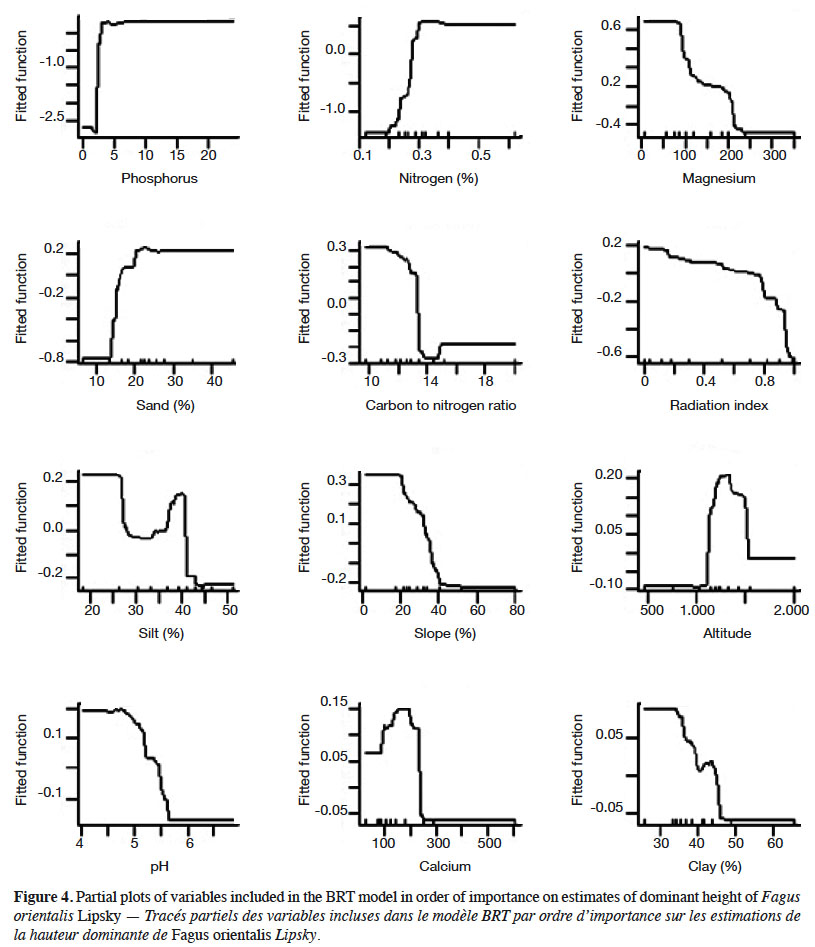
17The partial dependency plots of the most important variables in BRT technique in beech dominant height variation showed that the higher dominant height is obtained when phosphorus and organic matter increase. Partial dependence plots representing the marginal effect of single variables using BRT model on estimates of beech dominant height are shown in Figure 4.

4. Discussion

18In the present study, we evaluated the dominant height of oriental beech, which is one of the most abundant species in the Hyrcanian forests of Iran, using a boosted regression tree model and edaphic and topographic variables. Like other studies (Lawler et al., 2006; Leathwick et al., 2006; Moisen et al., 2006; Prasad et al., 2006; Benito Garzón et al., 2008; Lawler et al., 2009; Pittman et al., 2009; Aertsen et al., 2010; Knudby et al., 2010; Leclere et al., 2011; Vincenzi et al., 2011; Oppel et al., 2012; França & Cabral, 2015), in this research, application of ensemble technique (boosted regression trees) provides an effective methodology for predicting the beech dominant height in Hyrcanian forests. Elith et al. (2008) highlighted some main advantages of BRT approach including strong predictive performance, reliable identification of relevant variables and interactions. The increasing growth of BRT application in ecological studies is a witness for its efficiency (Elith et al., 2006; Leathwick et al., 2006; Elith et al., 2008; Pittman et al., 2009; Aertsen et al., 2010; Froeschke & Froeschke, 2011; Aertsen et al., 2012; Kint et al., 2012). Differences in model performances may be attributed to their inherent properties. There are a certain number of assumptions in linear regression including normality, homoscedasticity, independence of variables and model linearity that are rarely met by these models (Zuur et al., 2009), but tree-based approaches may overcome these difficulties. Contrary to linear models, in machine learning techniques an algorithm is used in order to learn the relationship between the response and explanatory variables, then dominant patterns in data are found via the inputs and response observations, not a priori, and finally the model structure is developed as a direct function of that particular dataset (Miller & Franklin, 2002; Elith et al., 2008; França & Cabral, 2015). Although classification and regression trees are inherently simple and interpretable, they have a major drawback; a small change in the data can often prompt to extensive changes in the form of the fitted tree. Therefore, it is somewhat difficult to interpret these trees reliably. This is the downside of such a simple model structure, thus ensemble methods could be used for solving these problems (Simpson & Birks, 2012). The results of this study also showed ensemble methods are preferred and superior techniques for predicting response variables and their superiority is attributed to the incorporation of nonlinearity and interaction effects, because they are important features and lead to lower prediction errors.

19The application of boosted regression trees model for prediction purposes is particular useful when there are complex interactions between predictors and response variable (in our case the dominant height of F. orientalis) and the possibility of highly correlated predictor variables. Despite the fact that there were some systematic differences in performance among methods, the BRT method shows relatively similar and consistent patterns in predicting F. orientalis dominant height. Thus, we conclude that the dominant height of F. orientalis in the Hyrcanian forests can be successfully predicted using BRT nonlinear modelling techniques. Therefore, we use an ensemble approaches for further investigation.

20An important aspect in ecological modelling involves the evaluation and interpretation of the results. Phosphorus and nitrogen were the most important variables affecting the dominant height of beech tree species. Soil nitrogen and phosphorus are the most common macronutrients which limit the growth of plants under natural conditions (Liu et al., 2014). Phosphorus is of particular importance in accelerating the root growth, cell division, and growth of meristem tissues, its limitation is associated with a sharp decline in tree growth. As a result, phosphorus deficiency will slow down or stop the growth of above- and underground parts of the forest trees. The results of this study showed that with increasing nitrogen content, the dominant height of beech tree species also increases. On the other hand, beech tree has a decreasing behavior relative to the C/N variable. The ratio of carbon to nitrogen is one of the important indices of mineralization and soil fertility. Increasing nitrogen contents and decreasing carbon to nitrogen ratios increase the activity of soil microorganisms and accelerate the litter decomposition (Habibi Kaseb, 1992; Shabani et al., 2012); as a result, the growth of beech tree species increases. In the analysis of the response curve of beech tree, Alavi et al. (2017) concluded that NPK and C/N variables are effective indices on tree growth (Alavi et al., 2017).

21The performance of species along elevation gradient is governed by a series of interacting biological, climatic, and historical factors (Colwell & Lees, 2000). Further, elevation represents a complex gradient along which many environmental variables change simultaneously (Austin et al., 1996). Beech tree has the best performance at altitudes from 1,200 to 1,700 m a.s.l. which is consistent with Marvi Mohajer (1976). It seems these altitude ranges have optimum humidity conditions and high productivity which resulted from optimal combination resource availability (Rahbek, 1995; Rosenzweig, 1995). Having demands for cool climates, beech tree avoids lower altitudes, since they are warmer and drier. The major decline in beech performance at higher altitudes could be due in part to ecophysiological constrains, such as reduced growing season, low temperature and low ecosystem productivity in high elevation (Körner, 1998).

22It is evident that beech trees have better performance on north-northeast directions (typically the coolest and wettest orientations). In the Northern Hemisphere, south-facing slopes may receive as much as six times more solar radiation than north-facing slopes. Thus, the south-facing slopes have a more xeric environment, that is, warmer, drier and a more variable microclimate, than the mesic north-facing slopes (Nevo, 1997; Nevo, 2001). Beech tree has the best performance in gentle slopes. The slope degree is an essential feature of topography in relation to runoff and soil erosion. The runoff and soil loss intensity can vary with different slope gradients. Since the slope gradient is the main factor for controlling soil erosion, with increasing slope gradient, the amount of soil loss increases significantly (Koulouri & Giourga, 2007). Several authors have also confirmed the exponential influence of slope gradient on soil loss (Lal, 1976; Roose, 1977).

23Soil texture as an important soil characteristic determines the rates of water intake, water storage in the soil, the amount of aeration (vital to root growth) and influences the soil fertility. The effects of the textural properties of soils are frequently reflected in the composition and growth rate of forest vegetation (Sharma et al., 2010). The result of this study indicated percentage sand was a more important factor than clay in affecting the beech dominant height. The partial dependence plots for these two variables are also interesting. The partial plots for these variables show that the beech tree species has the best performances in low clay and medium sand contents, respectively which is consistent with the results of Tabari et al. (2005). While soils high in clay are difficult to manage because of their great strength and sticky nature, an intermediate amount of clay in a soil improves its capacity to hold water and plant nutrient ions. A balanced combination of sand, silt and clay composition makes loamy soil, which is the best one for the plant growth (Pidwirny, 2004) and support the luxuriant vegetation.

24This research also shows that the high pH values are a limiting factor on the dominant height of beech tree. pH of the soil directly or indirectly affects the growth of the tree species. The most important role of soil pH is controlling the solubility of nutrients in the soil. In other words, the ability to absorb nutrients is highly dependent on soil pH. Nutrients have different solubility at different pH values. Usually, by increasing the pH values, the solubility of the essential nutrients for the plant growth is reduced, and the deficiency of nutrients such as phosphorus, iron, zinc and manganese in the plant can be observed (Salardini, 2011; Alavi et al., 2017).

5. Conclusions

25Boosted regression tree model was used for evaluation of beech dominant height in Hyrcanian forests. Our assessment of the mentioned techniques based on two measures of accuracy showed that boosted regression tree model has high performance in reducing the prediction error of dominant height variable in these forests. The high flexibility of this model is attributed to its ability for incorporating the nonlinear and interaction effects. The boosted regression trees method with low RMSE has a good accuracy for predicting beech dominant height in the Hyrcanian forests. By reviewing the literatures and the response curves resulted from the different modelling approaches, the response curves of BRT also have better ecological interpretability and rationality. Boosted regression tree technique indicated that phosphorus, percentage nitrogen, magnesium and percentage sand were among the most important variables in predicting the dominant height of beech tree species in the study area. There are other modelling techniques, for example, Multiple Adaptive Regression Splines and Artificial Neural Networks that should also be considered for future evaluations of model performance, since their applications in ecological modelling studies have been gradually increasing. Nonetheless, in these techniques, the scientists have not much control over model fitting, and it is difficult to assess the relative importance of individual explanatory variable. Overall, machine learning techniques help researchers gain more insights, both in terms of ecological relationships and species spatial distributions specially in terms of forest modelling and yield tables. They are now considered as a valuable tool for improving ecological management and biodiversity conservation.

Bibliographie

Om dit artikel te citeren:

Over : Seyed Jalil Alavi

Over : Kourosh Ahmadi

Over : Carsten F. Dormann

Over : Josep M. Serra-Diaz

Over : Zahra Nouri